Broadly spiralling shape from partial sums of Zeta (0.5 + i t)

[Swamp Thing]

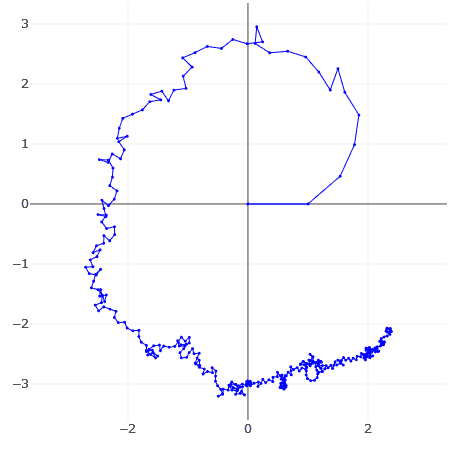
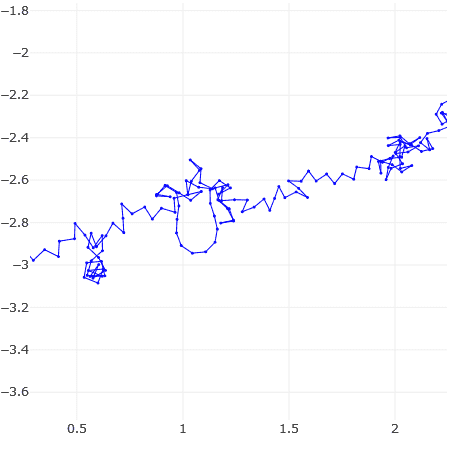
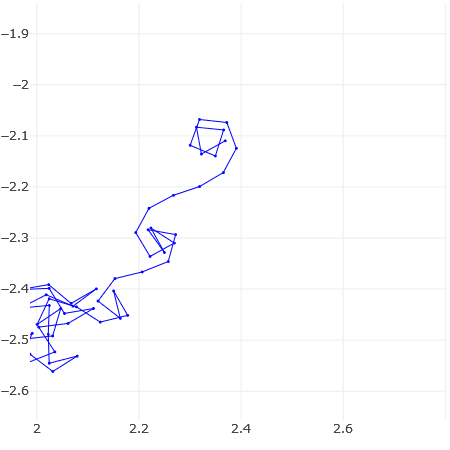
The first plot shows a large number of terms of Zeta(0.5 + i t) plotted end to end for t = 778948.517. The other plots are two zoomed-in regions, including one ending in a Cornu spiral. Despite all sorts of vicissitudes, the plot generally spirals outwards in a "purposeful" sort of way. It is not hard to find values of t that give such plots.

What causes this phenomenon?

Now for the first few terms, it can be explained as an aliasing effect where successive terms have approximately the same phase (angle) modulo 2 Pi. Similarly, the Cornu spiral is also an aliasing / sampling effect where the angle modulo 2Pi changes gradually.

But what about the emergence of a broad trend from a really long series of terms that seem to be changing randomly in angle?

 

[pbuk]

The first plot shows a large number of terms of Zeta(0.5 + i t)

I assume you are referring to the Riemann zeta function? How are you defining a 'term' of $\zeta(s)$?

 

[Swamp Thing]

Yes, it's the Riemann zeta function.
So the Nth term would be N^( -s ) ?

 

[pbuk]

Ah, I thought that might be the case. That definition only holds for $\mathfrak{Re}(s) > 1$.

 

[Swamp Thing]

Ah, I thought that might be the case. That definition only holds for $\mathfrak{Re}(s) > 1$.

This has been nagging at my mind. Is it technically wrong to talk of "partial sums" (and their "terms"), for a divergent series that has to be evaluated by analytical continuation?

 

[Swamp Thing]

Update: shortly after posting the OP, I realized that by tweaking the "t" value a bit, the spiral can be straightened out so that it runs in an approximately straight path. This happens whenever the magnitude of zeta(s) goes through a particularly tall peak.

This doesn't quite answer my original question, though.

 

[pbuk]

This has been nagging at my mind. Is it technically wrong to talk of "partial sums" (and their "terms"), for a divergent series that has to be evaluated by analytical continuation?

It is not wrong to talk about partial sums of a divergent series, however the analytic continuation of $\zeta(s)$ does not relate to that series. Or to put it another way, the partial sums of the series $\displaystyle\sum_{n = 1}^{\infty} \frac{1}{n^s}$ may or may not be interesting in their own right but they have nothing to do with $\zeta(s)$ when $\mathfrak{Re}(s) \le 1$.

 

[Swamp Thing]

partial sums of the series ... have nothing to do with ζ(s) when Re(s)≤1.

Would it be considered startling or original if this disconnect could be bridged?

The reason I ask is that for a couple of years I have been doing numerical experiments and stuff, based on which I hope to make some YouTube videos that will explain how to understand analytic continuation by starting with the partial sums and some of their properties. The aim is to target people with very basic calculus and complex number prerequisites. (Maybe I will write an Insights article on PhysicsForums at some point).

 

[pbuk]

Would it be considered startling or original if this disconnect could be bridged?

If by 'bridging' you mean subtracting $\displaystyle\sum_{n = 1}^{\infty} \frac{1}{(2n)^s}$ so that you get the Dirichlet eta function and an extension of the region of convergence to $\mathfrak{Re}(s) \gt 0, s \ne 1$ then that would not be startling or original. It might be interesting to see how the partial sums of $\eta(s)$ behave, but the partial sums of $\eta(s)$ don't look like the partial sums of $\displaystyle\sum_{n = 1}^{\infty} \frac{1}{n^s}$ in the region we are interested in.