C2-solutions to a diff.equation.

[Hatmpatn]

I have the following problem:
----------------------
Calculate all the C2-solutions z(x,y) to the differential equation:

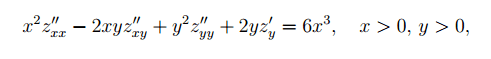
with the following constraint:

by making the substitution u=xy, v=x

------------------------

Solution
I've begun slightly but this doesn't take me far..

 

[pasmith]

Start by working out what the differential operators $\frac{\partial}{\partial x}$ and $\frac{\partial}{\partial y}$ are in terms of $u$, $v$ and the differential operators $\frac{\partial}{\partial u}$ and $\frac{\partial}{\partial v}$. From these you can find expressions for the second-order operators.

Now substitute these expressions into the original PDE, and tidy up the result. You should find that most of the terms cancel.