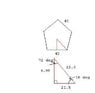
SUMMARY
The area of a regular pentagon with a perimeter of 215 feet can be accurately calculated using the formula for the area of a regular polygon: A = 1/2 * a * p, where 'a' is the apothem and 'p' is the perimeter. In this case, the apothem is determined to be 59.2 feet, resulting in an area of 6362 square feet. Alternatively, a simplified method involves squaring the length of one side (43 feet) and multiplying by 1.7205, yielding an area of approximately 3181.2045 square feet. This discussion highlights the importance of using precise geometric properties for accurate area calculations.
PREREQUISITES
- Understanding of regular polygons and their properties
- Familiarity with geometric formulas for area calculation
- Knowledge of trigonometric functions, particularly tangent
- Basic arithmetic and algebra skills for calculations
NEXT STEPS
- Research the derivation of the apothem formula for regular polygons
- Learn about the properties of regular pentagons and their symmetry
- Explore advanced geometric calculations involving trigonometry
- Investigate the application of area calculations in construction and landscaping
USEFUL FOR
Mathematicians, architects, engineers, and anyone involved in construction or landscaping projects requiring precise area calculations for polygonal shapes.