Calculate Data Points to Match Given Totals

[micromichele]

Hello! I have a super tricky problem for everyone I truly hope there is an answer to this.

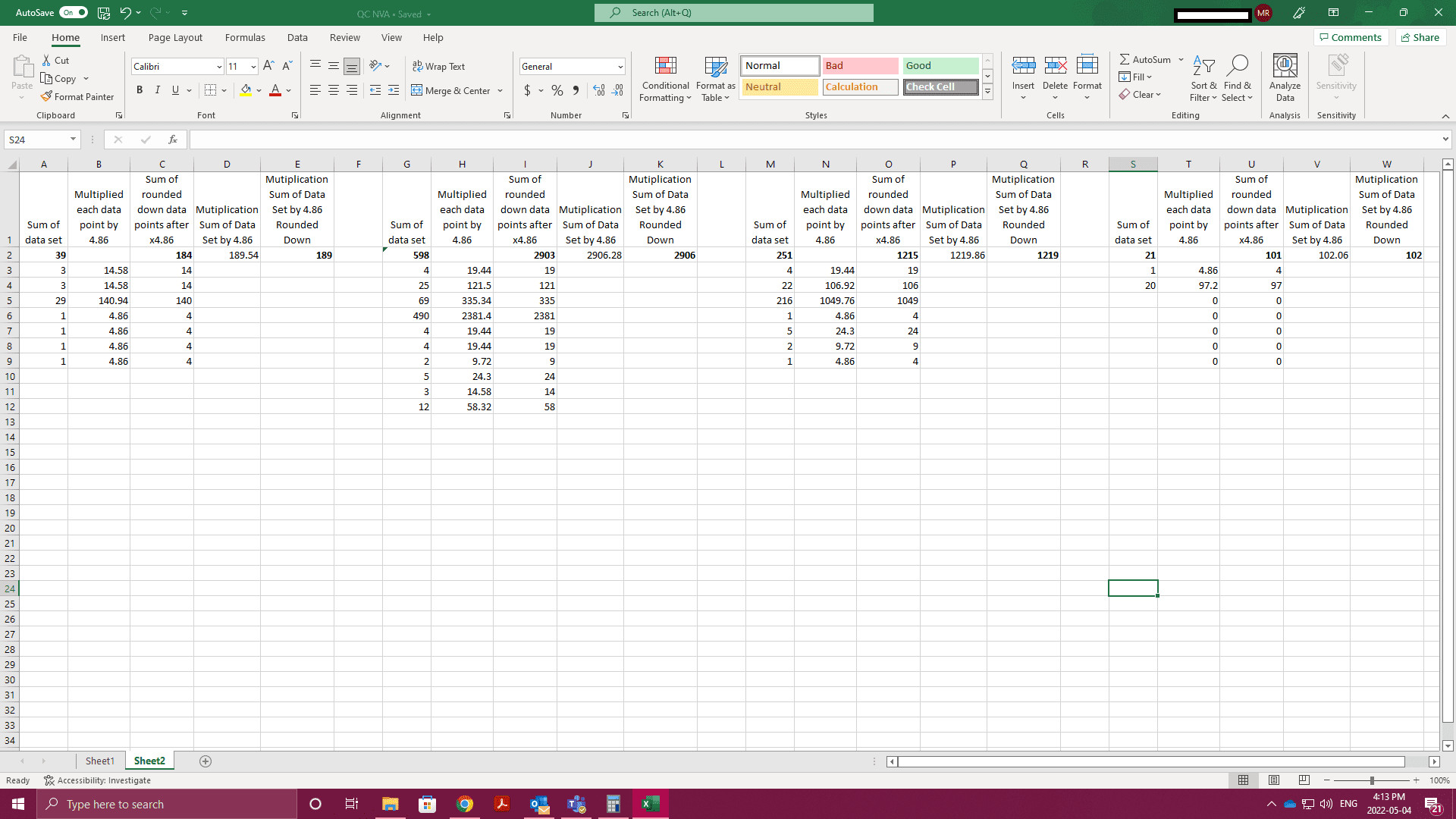
I have different data sets all of which are a different amount of number per set (total points per set)
Each number is multiplied by 4.86 then rounded down. Then the total is added

Alternatively the sum of the data points is multiplied by 4.86 then rounded down.

Just to add another note in case it was confusing so first set
189 needs to be 184
second set
2906 needs to be 2903
third
1219 needs to be 1215
fourth
102 needs to be 101

I need these two numbers to match and I can not figure out how I have attached a photo to help with this.

 

[Evgeny.Makarov]

Let's denote the result of rounding down $x$ by $\lfloor x\rfloor$. This operation and addition do not commute, which means that in general $\lfloor x_1+x_2\rfloor\ne\lfloor x_1\rfloor+\lfloor x_2\rfloor$. One can only guarantee that $\lfloor x_1+x_2\rfloor\ge\lfloor x_1\rfloor+\lfloor x_2\rfloor$. The same holds for more than two numbers. Here $x_i$ denote the numbers from you datasets multiplied by 4.86. Therefore your mismatches are expected (provided the computations are correct), and you cannot make the results to coincide any more than you can make 2 + 2 equal 5.

 

[I like Serena]

A possible solution is to not round down.
It is good practice to never round intermediate results. And final results are usually rounded to appropriate precision only for display.
In Excel you can format fields to show data with a desired precision while the calculations still work with unrounded numbers.

 

[micromichele]

Thank you for you replies and help :)