SUMMARY
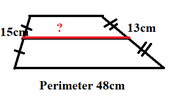
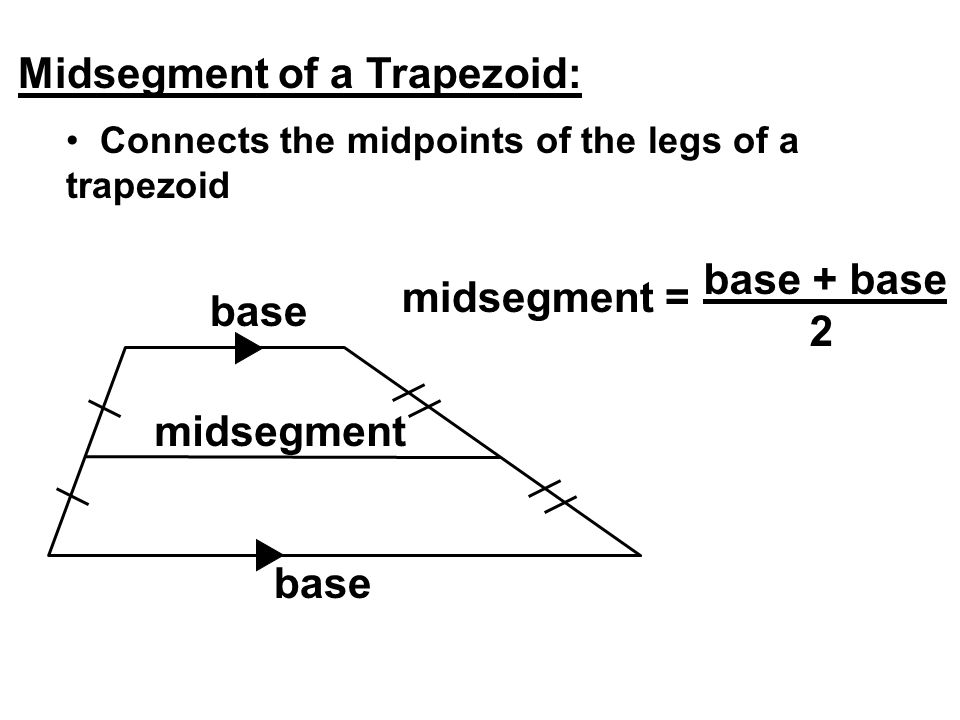
The discussion focuses on calculating the length of the median of a trapeze with a perimeter of 48 cm and non-parallel sides measuring 15 cm and 13 cm. The sum of the lengths of the two parallel bases is determined to be 20 cm. The median, or mid-segment, is defined as the average of these two base lengths. Therefore, the length of the median is the average of the two bases, which is the final answer sought by the participants.
PREREQUISITES
- Understanding of trapeze geometry
- Knowledge of perimeter calculations
- Ability to calculate averages
- Familiarity with basic algebraic equations
NEXT STEPS
- Study the properties of trapezoids and their medians
- Learn how to derive the lengths of bases from given perimeters
- Explore geometric mean calculations in trapezoids
- Practice solving problems involving trapezoidal dimensions
USEFUL FOR
Students studying geometry, mathematics educators, and anyone interested in understanding trapezoidal properties and calculations.