Calculate Water Pipe Surface Area & Volume - Ask an Expert

[Monoxdifly]

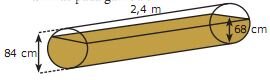
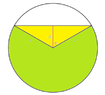
A water pipe whose diameter is 84 cm dan length is 2,4 m can contain rain water with the water height 68 cm like in the attached picture.
View attachment 8252
Determine:
a. The surface area which gets contact with the water
b. The volume of the water (in liters)

So... How do I do? What is the simple way to determine the area of a... truncated circle? (dunno what the proper term is)

 

[HOI]

How many boards have you posted this to? On "My Math Forum" I wrote

Looks like a pretty standard Calculus II problem. Start by drawing a cross section of the pipe on a coordinate system- a circle with center at (0, 0) and diameter 84, so radius 42, has equation [math]x^2+ y^2= 42^2[/math]. The bottom of that circle is at y= -42, the top is at y= 42. The surface of the water is a horizontal line at y= 68- 42= 26. At every y, a horizontal line intersects the circle at [math]x= \pm \sqrt{42^2- y^2}[/math] so has length [math]2\sqrt{42^2- y^2}[/math]. Taking a 'thickness' of [math]\Delta y[/math], the area of that thin horizontal strip is [math]2\sqrt{42^2- y^2}\Delta y[/math]. Adding those gives the Riemann sum, [math]\sigma 2\sqrt{42^2- y^2}\Delta y[/math], that, in the limit, is the integral for the area, [math]2\int_{-42}^{26}\sqrt{42^2- y^2}dy[/math].

 

[MarkFL]

Consider the following diagram:

View attachment 8253

To find the sum of the shaded areas, I would begin by finding the angle $\theta$ in terms of $h$ and $r$. Can you do that?

 

[Monoxdifly]

How many boards have you posted this to?

4 (MMF, MIF, MHB, and MHF).

Is there any approach without using calculus or trigonometry? This is supposed to be for 9 graders.

 

[Olinguito]

You don’t need calculus. I would use MarkFL’s approach as follows.

Find the angle $\theta$ (and make sure it’s in radians). The area of the yellow triangle in Mark’s diagram is $A_1=\frac12r^2\sin2\theta$. The area of the olive-green area below it is $A_2=\frac12r^2(2\pi-2\theta)$. So the area of the water in contact with one end of the pipe is $A=A_1+A_2$. Thus:

• The length of the major arc of the circle enclosing the olive-green area is $s=r(2\pi-2\theta)$. Hence the total surface area of water in contact with the pipe is $\boxed{2A+sL}$ where $L=240\,\mathrm{cm}$ is the length of the pipe. The answer here is in square centimetres.
  
  
• The volume of water is $\boxed{AL}$, which is in cubic centimetres so you’ll need to convert to litres: $1\,\mathrm{cm^3}\ =\ 0.001\,\ell$.

 

[Wilmer]

Lotsa good Chord stuff Mr.Fly:
Chord of a Circle | MathCaptain.com

 

[I like Serena]

Is there any approach without using calculus or trigonometry? This is supposed to be for 9 graders.

We can do (a) without calculus or trigonometry.
Starting with MarkFL's picture we need to find the size at the top.
We can do that with Pythagoras can't we?
The triangle has hypotenuse $\frac 12\cdot 84 = 42\text{ cm}$ and vertical side $68 - \frac 12 \cdot 84 = 26\text{ cm}$ doesn't it?

(b) is a bit more complicated. I think we really need the angle $\theta$ in Mark's drawing.
Then we can find the fraction of a circle disk that corresponds to $360^\circ - 2\theta$.
And we can add the area of the two triangles, which we can find from the numbers we found in (a).
Multiply with the length of the cylinder and we have the volume.

 

[Monoxdifly]

We can do (a) without calculus or trigonometry.
Starting with MarkFL's picture we need to find the size at the top.
We can do that with Pythagoras can't we?
The triangle has hypotenuse $\frac 12\cdot 84 = 42\text{ cm}$ and vertical side $68 - \frac 12 \cdot 84 = 26\text{ cm}$ doesn't it?

But what about the surface area?

 

[MarkFL]

But what about the surface area?

You've got the two ends of the pipe already, and then along the pipe of length \(L\) you have:

$$r(2\pi-2\theta)L$$