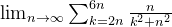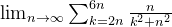SUMMARY
The discussion focuses on calculating limits using integrals, specifically approximating a series with an integral. Participants discuss the relationship between sums and integrals, particularly for strictly decreasing functions, and how to derive the integral of the function $$\frac{n}{k^2+n^2}$$. The correct limit is established as $$\arctan(6)-\arctan(2)$$ through the evaluation of a Riemann sum that corresponds to the integral $$\int_2^6\frac{1}{x^2+1}\,dx$$.
PREREQUISITES
- Understanding of Riemann sums and their relation to integrals
- Knowledge of calculus, specifically integration and differentiation
- Familiarity with the properties of the arctangent function
- Ability to manipulate and simplify mathematical expressions involving limits
NEXT STEPS
- Study the concept of Riemann sums in more detail
- Learn about the properties and applications of the arctangent function
- Explore techniques for approximating series with integrals
- Practice calculating limits involving integrals and series
USEFUL FOR
Students and professionals in mathematics, particularly those studying calculus, numerical analysis, or anyone interested in understanding the relationship between sums and integrals in limit calculations.