Calculate third point from 2 points and an angle

In summary, the conversation revolves around finding a third point that is rotated by a certain angle from two given points. The proposed method involves using trigonometric functions to calculate the coordinates of the third point. The person asking the question confirms that this method is correct.
  • #1
GamerVSL
2
0
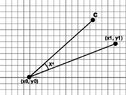
I'm having a hard time putting together a formula. I have 2 points (x0, y0) and (x1, y1) and an angle (k).
Using this information I need to calculate a third point that is k degrees from the previous 2 points.
View attachment 7880
Is it possible to do that? Thank you for your attention.
 

Attachments

  • problema_code.jpg
    problema_code.jpg
    32 KB · Views: 72
Mathematics news on Phys.org
  • #2
From your diagram, it looks as though the point C is found by rotating (x1,y1) about (x0,y0) by an angle of x degrees. Is this what you want? If so, there are standard ways of doing this problem. If you need further help on this, post again.
 
  • #3
I found a method:

Cx=cos(θ)⋅(X1−X0)−sin(θ)⋅(Y1−Y0)+X0
Cy=sin(θ)⋅(X1−X0)+cos(θ)⋅(Y1−Y0)+Y1

Is it right?
 
  • #4
Yes, this rotates (x1,y1) about (x0,y0) through an angle of $\theta$.
 

FAQ: Calculate third point from 2 points and an angle

How do I calculate the third point from 2 points and an angle?

To calculate the third point, you will need the coordinates of the first two points and the measure of the angle between them. Using trigonometry, you can determine the distance and direction of the third point from the second point. Once you have these values, you can add or subtract them from the coordinates of the second point to find the coordinates of the third point.

What is the formula for calculating the third point?

The formula for calculating the third point from 2 points and an angle is as follows:
x3 = x2 + d * cos(θ)
y3 = y2 + d * sin(θ)
where x3 and y3 are the coordinates of the third point, x2 and y2 are the coordinates of the second point, d is the distance between the second and third point, and θ is the angle between the two points.

Can I use any unit of measurement for the angle?

Yes, you can use any unit of measurement for the angle as long as you are consistent with it throughout the calculation. For example, if you use degrees for the angle, you must also use degrees for the trigonometric functions (cos and sin) in the formula. Similarly, if you use radians for the angle, you must use radians for the trigonometric functions.

Is it possible to calculate the third point if the angle is not given?

No, it is not possible to calculate the third point if the angle is not given. The angle is a crucial piece of information needed to determine the distance and direction of the third point from the second point. Without it, the calculation cannot be completed.

Can I use this formula to calculate the third point in any coordinate system?

Yes, you can use this formula to calculate the third point in any coordinate system as long as you use the same coordinate system for all points. For example, if the first two points are in Cartesian coordinates, the third point must also be in Cartesian coordinates for the calculation to be accurate.

Similar threads

MHB Find the Bearing from A to C & Angle B: Solve Here
Replies
3
Views
2K
B Reprise: Calculate the distance between two points without using a coordinate system
Replies
1
Views
1K
I Formula For Calculating Field Angle (Beam Angle) of Light?
Replies
2
Views
2K
MHB Calculating Height and Distance of a Mountain at Sea
Replies
8
Views
2K
Measurement of Angles and Lengths With Length Contraction
Replies
11
Views
722
MHB Finding the Equation of a Circle Passing Through Three Given Points
Replies
7
Views
3K
MHB What are the coordinates of points equidistant from (1,0) and (5,4)?
Replies
6
Views
1K
MHB Angle calculation in a sloping vector system
Replies
1
Views
1K
MHB Square metric not satisfying the SAS postulate
Replies
3
Views
4K
MHB Distance between points question
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top