- #1
mikejm
- 40
- 2
I am trying to solve for the theoretical relative decay rates of the various (m,n) modes of an ideal circular membrane, if that membrane is excited momentarily by an impulse or deformation.
I would ideally like the decays of the (m,n) modes in dB/s.
Imagine a simple isolated drum head being struck by a stick. The membrane should be considered fixed with even tension around its perimeter. The excitation impulse/deformation should be at its center or x*radius from its center.
Someone on another site said of this problem:
The wave equation for modes of an ideal circular membrane is given by:
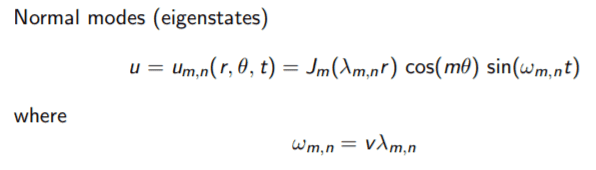
The full wave equations are described/explained further in these documents:
http://www.math.ubc.ca/~nagata/sci1/drum.pdf
https://courses.physics.illinois.ed...P406POM_Lecture_Notes/P406POM_Lect4_Part2.pdf
http://ramanujan.math.trinity.edu/rdaileda/teach/s12/m3357/lectures/lecture_3_29.pdf
I can use the Bessel zeros to calculate the frequencies of the various (m,n) modes and have done so already. However, I am unsure how to get the decay rates for these modes as he describes.
Does the method he suggests make sense? If so, can anyone elaborate further on how I would go about doing this? Or is there a better way?
Ideally I'd like an equation I can put in (m,n) for, plus perhaps an arbitrary constant damping coefficient, and get the decay of that mode in dB/s. If the decay rate of any mode might vary depending on the point of excitation, some way to specify for excitation position might be useful.
Thanks for any help!
I would ideally like the decays of the (m,n) modes in dB/s.
Imagine a simple isolated drum head being struck by a stick. The membrane should be considered fixed with even tension around its perimeter. The excitation impulse/deformation should be at its center or x*radius from its center.
Someone on another site said of this problem:
If the air damps it linearly enough, you can probably solve it analytically. Use plate theory to generate a PDE, then work out all the eigenmodes. The decay rate will be determined by the real components of the eigenvalues, and can be converted into dBs-1 using a few logs.
The wave equation for modes of an ideal circular membrane is given by:
The full wave equations are described/explained further in these documents:
http://www.math.ubc.ca/~nagata/sci1/drum.pdf
https://courses.physics.illinois.ed...P406POM_Lecture_Notes/P406POM_Lect4_Part2.pdf
http://ramanujan.math.trinity.edu/rdaileda/teach/s12/m3357/lectures/lecture_3_29.pdf
I can use the Bessel zeros to calculate the frequencies of the various (m,n) modes and have done so already. However, I am unsure how to get the decay rates for these modes as he describes.
Does the method he suggests make sense? If so, can anyone elaborate further on how I would go about doing this? Or is there a better way?
Ideally I'd like an equation I can put in (m,n) for, plus perhaps an arbitrary constant damping coefficient, and get the decay of that mode in dB/s. If the decay rate of any mode might vary depending on the point of excitation, some way to specify for excitation position might be useful.
Thanks for any help!