Calculating Diffusion Velocity in Electrochemical System

[ussername]

Let's suppose an electrochemical system with given coordinates:

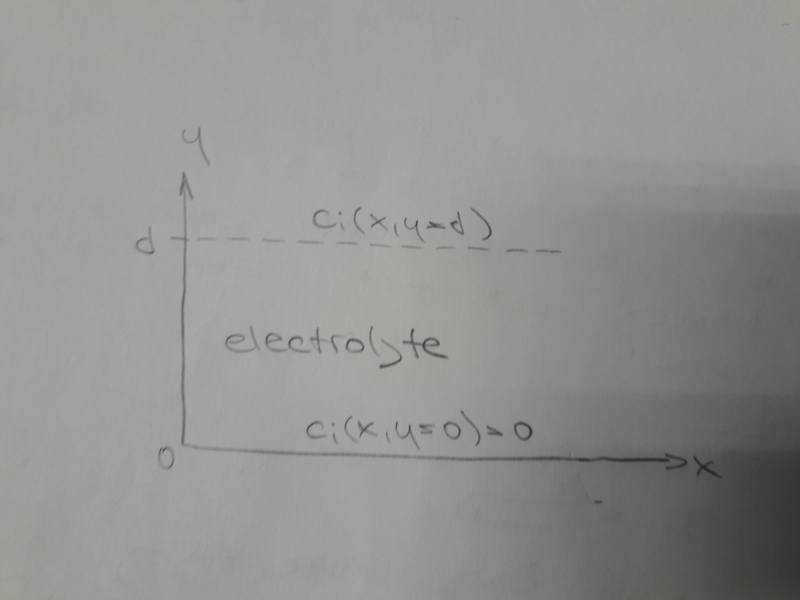
We are interested in diffusion motion of ion $i$ in the direction of $y$ axis.
Concentration $c_i$ is a function of both $x$ and $y$. Concentration $c_i$ at $y=0$ is zero.
The system is steady thus $\frac{\partial c_i}{\partial y}(x)$ is not a function of $y$ ($\frac{\partial c_i}{\partial y}(x)$ is constant with $y$).
The first Fick's law for ion $i$ is (for simplicity I don't write $i$ subscript anymore):
$$J_{y}^{dif}(x,y=d) = - D \cdot \frac{\partial c}{\partial y}(x,y=d) = - D \frac{c(x,y=d)}{d}$$
The diffusion molar flux is:
$$J_{y}^{dif}(x,y=d) = c(x,y=d)\cdot v_{y}^{dif}(x,y=d)$$
where $v^{dif}$ is the diffusion linear velocity of ion $i$:
$$v_{y}^{dif} = -D \cdot \frac{1}{c}\cdot \frac{\partial c}{\partial y}$$
The diffusion velocity clearly changes because concentration changes with $y$.
Now I can put the diffusion velocity into the first equation and express $D$:
$$D = \frac{-c(x,y=d)\cdot v_{y}^{dif}(x,y=d)\cdot d}{c(x,y=d)}=-v_{y}^{dif}(x,y=d)\cdot d$$
This seems strange to me. Since both diffusion coefficient $D$ and length $d$ are considered constant, the diffusion velocity $v_{y}^{dif}(x,y=d)$ seems to be constant along $x$ independently of the functions $c(x) \ at \ y=d$ and $\frac{\partial c}{\partial y}(x) \ at \ y=d$. Is it true?

 

[Henryk]

I strongly object to the term 'diffusion linear velocity'. Diffusion is due to random (Brownian) motion of molecules and other particles so what exactly is moving with 'diffusion linear velocity'? how would you measure it?
It makes no sense.
What you do have is Flick's law and it is a differential equation. Add initial and boundary condition, solve it and you have all the answers.
By the way, the diffusion equation is linear.

 

[ussername]

I found this problem when I was trying to derive the relation for diffusion time of ion $i$:
$$\tau^{dif} = \frac{d^2}{D}$$
In order to understand what $\tau^{dif}$ really means, it is useful to define $v^{dif}$.

By the way $v^{dif}$ can be measured no worse than for example molar fluxes of diffusion, migration or convection. It can be measured when the diffusion motion prevails.

 

[Lord Jestocost]

I found this problem when I was trying to derive the relation for diffusion time of ion $i$:
$$\tau^{dif} = \frac{d^2}{D}$$

When considering random-walk diffusion (for example in one dimension), the equation
<x ²> = 2 D t
relates the mean square displacement <x ²> of diffusing particles with the elapsed time t. Here it is assumed that the particles start out at position x = 0 at time t = 0.
Roughly speaking, a particle with a diffusion coefficient D diffuses thus a distance d in a time t ≈ d ²/2D.