Calculating Land Area for an Olympic Track: A Linear Equation Application

[bergausstein]

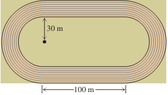
Olympic Track. To host the Summer Olympics, a city plans to
build an eight-lane track. The track will consist of parallel 100-m
straightaways with semicircular turns on either end as shown in
the figure. The distance around the outside edge of the oval track
is 514 m. If the track is built on a rectangular lot as shown in
the drawing, then how many hectares (1 hectare = 10,000 m^2)
of land are needed in the rectangular lot?

I've got no Idea where to start first. please help me. thanks!

 

[Evgeny.Makarov]

Let's denote the radius of the outside edge of the semicircular turn by $R$. (According to the picture, the similar radius of the inner edge of the turn is 30m, but this is not used in the solution.) Express the length of the outside edge of the turn through $R$. Next, express the length of the whole outside edge (it consists of two straight segments with length 100m each and two semicircular turns). Equate the result to 514m and find $R$ from the equation.

 

[bergausstein]

let r = the total perimeter of the two semicircles
the distance of the outside edge of the track is

514=200+r

r = 314

since C=2pi*R

314 = 2pi*(30+R)

the radius of the outer edge is R = (314-60pi)/2pi

what's next?

 

[Evgeny.Makarov]

let r = the total perimeter of the two semicircles

It's kinder to the reader to denote the perimeter by something like $p$ and radius by something like $r$.

the distance of the outside edge of the track is

514=200+r

r = 314

since C=2pi*R

314 = 2pi*(30+R)

In the last two lines, you used $R$ in two different senses. I undersand that $C$ and $R$ in $C=2\pi R$ are probably generic circumference and radius, i.e., not necessarily from this problem, but still it's a bad style. Besides, in writing $314 = 2\pi(30+R)$ you denoted by $R$ the total width of the lanes, while my suggestion was to use it to denote the external (greater) radius of the turn. The width could be denoted by something like $w$.

Anyway, I believe the number 314 is used on purpose to suggest diving both sides by $\pi$. From this you get $30+R$--the external radius of the turn. Then finding the width and length of the lot should be obvious.

 

[bergausstein]

Can you show me how you would solve it.

 

[Evgeny.Makarov]

If $R$ is the external radius, then $314=2\pi R$. Dividing by $\pi$, we get approximately $100=2R$, or $R=50$. Therefore, the length of the lot is $100+2 R=200$, and the width is $2R=100$.

 

[bergausstein]

If $R$ is the external radius, then $314=2\pi R$. Dividing by $\pi$, we get approximately $100=2R$, or $R=50$. Therefore, the length of the lot is $100+2 R=200$, and the width is $2R=100$.

yes the answer is approximately 2 hectares. thanks!