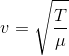zengodspeed
- 15
- 0
Homework Statement
A second harmonic standing wave has the known quantities of Amplitude (max y at antinode) A, maximum velocity (y=0 at antinode) v, string length L, tension in the string T.
Given that we know that it is second harmonic, we can assume that λ = L
How can one determine the mass of the string?
Homework Equations
The Attempt at a Solution
Attempt at solution:
Using the equation to solve for velocity:
I know that I can find the mass of the object if I can find the wave speed, but without knowing the frequency/period of the wave I do not see how I can find this.
Thanks in advance