Calculating Mercury Column Height in J-Shaped Tube: Manometry Homework Solution

[Queren Suriano]

Homework Statement

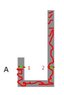
A J-shaped tube has an uniform cross section and it contains air to atmosphere pression of 75 cmo of Hg. It is pours mercury in the right arm, this Compress the closed air in the left arm. Which is the heigh of the mercury's column in left arm when the right arm is full of mercury? Consider that in every moment temperature is constant and that the air is an ideal gas. Consider h1 = 0.25m and h2 = 2.25m

2. Relevant equations

P= Patm + density*g*h
P1*V1 = P2*V2

The Attempt at a Solution

I have equalized the pressure at point 1 with the pressure at point 2, and this looks like this:
Pressure at point 1 = Air density * gravity * (0.25-h)
Pressure at point 2 = Atmospheric pressure + mercury density * gravity* (2.25-h)

The atmospheric pressure I suppose is 75 cm Hg.

From previous equations I would solve for "h"

My question is if the approach is right? and how I could consider the density of the air?

Could I solve the problem by applying theory of ideal gases? thanks for your help

 

[kuruman]

Yes, you can use the ideal gas law, but you have to make some assumptions about how the mercury fills the tube. I suspect the amount of air trapped in the left arm originally occupied the entire left arm at atmospheric pressure. Your diagram does not show what h1 and h2 are. I assume they are the height of the mercury columns in the two arms. Correct?

 

[Queren Suriano]

Yes, you can use the ideal gas law, but you have to make some assumptions about how the mercury fills the tube. I suspect the amount of air trapped in the left arm originally occupied the entire left arm at atmospheric pressure. Your diagram does not show what h1 and h2 are. I assume they are the height of the mercury columns in the two arms. Correct?

NEW
Kuruman thank you for your answer. h1 and h2 are the length of left and right arm respectively. So, how can I solve the problem with ideal gas law? thank you

 

[kuruman]

NEW
Kuruman thank you for your answer. h1 and h2 are the length of left and right arm respectively. So, how can I solve the problem with ideal gas law? thank you

So you are saying that the left arm has length $y$ of air and length $h_1-y$ of mercury and the right arm has length $h_2$ of mercury. Correct?
You can use the ideal gas law to relate the final pressure of the air to the initial (atmospheric) pressure in the left arm. Note that the volume is proportional to the cross sectional area which does not change when the arm is partially filled with mercury.

 

[Queren Suriano]

So I can write Patm hinitial = P2 (0.25-h) where h is the heigh of compressed air. Me doubt is what is hinitial? Can I Convert the 75cm Hg to cm of air?

 

[kuruman]

Me doubt is what is hinitial?

Did you not tell me in post #3 that h_initial is the length of the left arm, 0.25 m?

 

[Queren Suriano]

Did you not tell me in post #3 that h_initial is the length of the left arm, 0.25 m?

Ok, thank you. So, am I saying something right if I said that P1 = Patm + air density * gravity* h1? Or could I assume that the P1 = Patm?

 

[kuruman]

I think it is safe to assume that p₁ = p_atm.