Ben Reade
- 11
- 0
Hello,
Firstly thank you for reading my post.
This is an interesting question I was wondering if anyone here could teach me how to work out.
Say if you had a large go-kart (FSAE/Formula Student if anyone knows of that) and you were driving at 120kph and hit the brakes and stopped in 3 seconds, how much force is going through the suspension spring/dampener.
Similarly what if it is going around a corner with a radius of 7.7kph at 80kph.
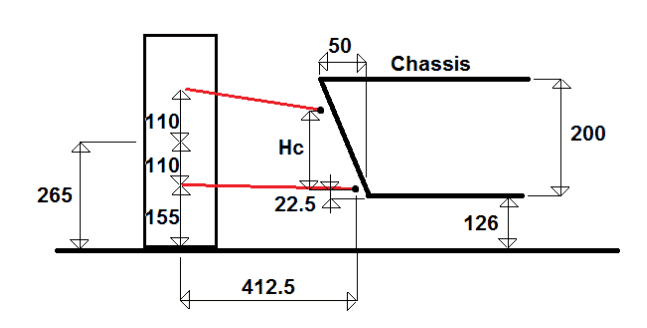
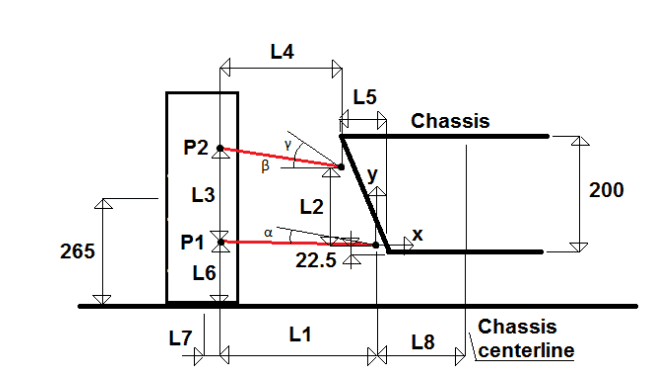
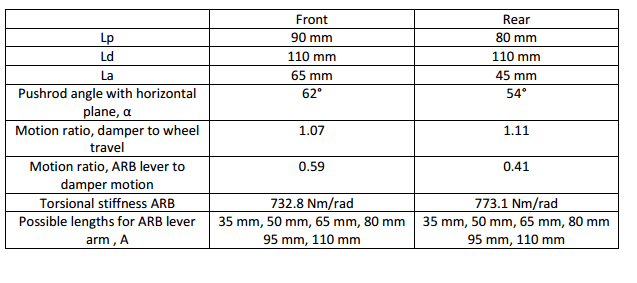
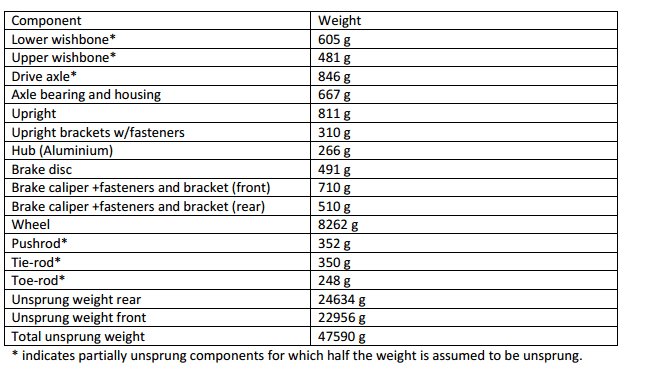
Here is a diagram of what I am talking about. Its double A-Arm wishbone suspension, along with any data you will need, such as weights and dimensions.



cough cough http://brage.bibsys.no/xmlui/bitstream/handle/11250/183058/Master oppgave-endelig.pdf?sequence=1
Firstly thank you for reading my post.
This is an interesting question I was wondering if anyone here could teach me how to work out.
Say if you had a large go-kart (FSAE/Formula Student if anyone knows of that) and you were driving at 120kph and hit the brakes and stopped in 3 seconds, how much force is going through the suspension spring/dampener.
Similarly what if it is going around a corner with a radius of 7.7kph at 80kph.
Here is a diagram of what I am talking about. Its double A-Arm wishbone suspension, along with any data you will need, such as weights and dimensions.
cough cough http://brage.bibsys.no/xmlui/bitstream/handle/11250/183058/Master oppgave-endelig.pdf?sequence=1