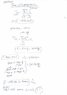- #1
marellasunny
- 255
- 3
(To the moderator,please don't shift to the Homework thread list.This thread explores the conceptual part of gear changes)
A 2 liter engine has T(max)=185Nm at [itex]\omega_e[/itex]=4500 rpm, has a manual gearbox with the following gear ratios:
n1=3.42,
n2=2.14,
n3=1.45,
n4=1.03,
n5=0.81,
nr=3.46,
nd=4.06; (final gearing ratio,has to be included in all calculations)
I find the radius of the car tires as 0.319m(as this is a Ford Mondeo which uses tires specified as 205/55/R16). I am asked to determine the gear speed equations for each gear:
$$\omega_e=\frac{n_in_d vx}{R_w}$$
$$T_e=\frac{R_wF_x}{\eta n_in_d}$$
I'm assuming [itex]\eta[/itex], the driveline efficiency is 1.
(My attempted solutions and understandings are attached as thumbnails)
Q.My question is on what rpm range do I base my power band(i.e the min and max rpms between which the gears change) [itex]\omega_1[/itex][itex]\omega_2[/itex]?
I'm thinking of using the minimum rpm at which the driver must gear down as 4500rpm(i.e the rpm value at Torque(max)), the reasoning for this is at the end. But,I do not know the maximum rpm at which the driver must gear-up(which I presume is the rpm at max power ??). How do I find this out?
Normally, I can find the rpms at which the gear changes must occur from the rpm at which max.power [itex]\omega_{Pmax}[/itex] occurs. i.e I use this value of this rpm to then calculate the [itex]\omega_1, \omega_2[/itex] at which the gear changes must occur, by using the equation [itex] \omega_{Pmax}=\frac{\omega_1+\omega_2}{2}[/itex].
This excerpt was taken from a very good article I read and it related to my idea of using the minimum rpm at which gearing down must occur[itex]\omega_1[/itex] as the max torque rpm[itex]\omega_{Pmax}[/itex]:
A vehicle engine operating at a rotational speed above its maximum-torque point is in a "stable" speed regime. If it slows down by a small amount (due to the vehicle encountering an incline, head-wind, etc.) engine torque will tend to increase and resist the slowing. Conversely, if it speeds up by a small amount, torque will tend to decrease and discourage a further increase in speed.
A 2 liter engine has T(max)=185Nm at [itex]\omega_e[/itex]=4500 rpm, has a manual gearbox with the following gear ratios:
n1=3.42,
n2=2.14,
n3=1.45,
n4=1.03,
n5=0.81,
nr=3.46,
nd=4.06; (final gearing ratio,has to be included in all calculations)
I find the radius of the car tires as 0.319m(as this is a Ford Mondeo which uses tires specified as 205/55/R16). I am asked to determine the gear speed equations for each gear:
$$\omega_e=\frac{n_in_d vx}{R_w}$$
$$T_e=\frac{R_wF_x}{\eta n_in_d}$$
I'm assuming [itex]\eta[/itex], the driveline efficiency is 1.
(My attempted solutions and understandings are attached as thumbnails)
Q.My question is on what rpm range do I base my power band(i.e the min and max rpms between which the gears change) [itex]\omega_1[/itex][itex]\omega_2[/itex]?
I'm thinking of using the minimum rpm at which the driver must gear down as 4500rpm(i.e the rpm value at Torque(max)), the reasoning for this is at the end. But,I do not know the maximum rpm at which the driver must gear-up(which I presume is the rpm at max power ??). How do I find this out?
Normally, I can find the rpms at which the gear changes must occur from the rpm at which max.power [itex]\omega_{Pmax}[/itex] occurs. i.e I use this value of this rpm to then calculate the [itex]\omega_1, \omega_2[/itex] at which the gear changes must occur, by using the equation [itex] \omega_{Pmax}=\frac{\omega_1+\omega_2}{2}[/itex].
This excerpt was taken from a very good article I read and it related to my idea of using the minimum rpm at which gearing down must occur[itex]\omega_1[/itex] as the max torque rpm[itex]\omega_{Pmax}[/itex]:
A vehicle engine operating at a rotational speed above its maximum-torque point is in a "stable" speed regime. If it slows down by a small amount (due to the vehicle encountering an incline, head-wind, etc.) engine torque will tend to increase and resist the slowing. Conversely, if it speeds up by a small amount, torque will tend to decrease and discourage a further increase in speed.
Attachments
Last edited: