Calculating the Speed of a Block After Moving Downward: Work and Energy Equation

[jjiimmyy101]

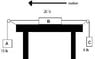
Question: The 20 lb block B rests on the surface of a table for which the coefficient of kinetic friction is 0.1. Determine the speed of the 10 lb block A after it has moved downward 2 ft from the rest. Neglect the mass of the pulleys and cords.

Picture Attached

Equation: T1 + Summation of work = T2

This is what I got.

s = displacement

0 + [(Force of Friction)*(s) - (Weight of A)*(s) - (Weight of C)*(s) = 0.5*mA*v^2 + 0.5*mB*v^2 + 0.5*mC*v^2

2*2 + 10*2 + 6*2 = 0.15528*v^2 + 0.31056*v^2 + 0.09317*v^2

38 = 0.55901*v^2
v = 8.24 ft/s

Is it right?

 

[Doc Al]

Originally posted by jjiimmyy101
v = 8.24 ft/s

Is it right?

You made an error with the signs of the work done to lift/lower the blocks. Since one raises and one lowers, the signs must differ.

To keep better track of signs, try thinking this way:
ΔKE + ΔPE = -(Work done against friction)

 

[jjiimmyy101]

Thanks! What a silly mistake. The answer is 6.27 ft/s!

 

[Doc Al]

Originally posted by jjiimmyy101
The answer is 6.27 ft/s!

I get a different answer. Recheck your numbers.