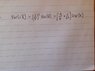Calculating Variance: Sample vs Population

[CAH]

See the photo of the question+ mark scheme!
I don't understand a question on finding an expression for the variance of something...

Attempt at solution: also I worked out c as (3/2) previously, which is correct
Var(U) = (3/2)^2 x Var(Xbar) = 9/4n^2 x a^2/18

I'll attach a photo of this too if it's easier to read, my problem is that I thought var(Xbar) = var(x/n) = 1/n^2 x var(x)

... But they have done var(Xbar) = 1/n x var(x) ...?

 

[statdad]

Think about this:
$$Var\left(\bar X\right) = Var\left(\frac 1 n \sum_{i=1}^n X_i\right) = \frac 1 {N^2} \sum_{i=1}^n Var(X_i)$$

What happens when you simplify the sum?

 

[CAH]

Ah I see so it's just sigma^2/n, is this the same for all cases as in, calculating the variance of a sample and estimating a population variance?.. In other words, kinda, will it ever (a level standard) be 1/n^2 x var(x)

Probably a stupid question, just checking

 

[statdad]

The only time you would have $n^2$ in the denominator is if you were (for some reason) considering mathematically a single observation $X_1$ and calculate
$$Var\left( \dfrac{X_1}{n}\right) = \dfrac{Var(X)}{n^2}$$

"is this the same for all cases as in, calculating the variance of a sample and estimating a population variance?"
I'm not exactly sure what you mean by this, so if my response is off-target that's why.

If you've talked about sampling distributions for the sample mean, the expression $\frac{\sigma^2}n$ is the population variance for that sampling distribution. It will never have denominator $n^2$, since, as long as the distribution being sampled has a variance, the steps shown above apply.

The (sample) variance of a sample is a different beast. Essentially
* if the population variance is $\sigma^2$, then the sample variance
$$s^2 = \dfrac 1 {n-1} \sum_{i=1}^n \, \left(x_i - \bar x\right)^2$$
is an unbiased estimator of the population variance

* If you refer to the variance of the sampling distribution of $\bar x$ - which is given above - then to estimate that you have two options
a) If you have a single sample, use the sample variance $$s^2$$ to estimate the sampling distribution's variance by calculating
$$\dfrac{s^2}{n}$$

b) If you have a large number of samples, all the same sample size, from the same population, then calculate each sample mean and treat those sample means as a new sample. The sample variance of those (call it $s_{\bar x}^2$) is the estimate of $\dfrac{\sigma^2}{n}$

So there are several subtleties to wade through, but in none but the one unusual and unrealistic comment I made at the start will $\frac{\sigma^2}{n^2}$ play a role.