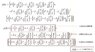SUMMARY
The differential equation dy/dx = y² + x² with the initial condition y(1) = 0 is identified as a Riccati Equation. The discussion highlights the transformation of this equation into a linear second-order ODE using the substitution y = -u'(x)/u(x). Participants emphasize the importance of correctly applying Bessel functions and avoiding common mistakes, such as misusing the properties of Bessel functions for non-integer orders. Ultimately, the analytical solution converges to y(2) = 6.703786022295645, aligning closely with numerical results obtained via the Runge-Kutta method.
PREREQUISITES
- Understanding of Riccati Equations
- Familiarity with Bessel functions and their properties
- Knowledge of numerical methods, specifically the Runge-Kutta method
- Basic proficiency in using mathematical software or online calculators for differential equations
NEXT STEPS
- Study the transformation techniques for Riccati Equations to linear ODEs
- Learn about the properties and applications of Bessel functions
- Explore the Runge-Kutta method in detail for solving differential equations
- Investigate online calculators and software that handle Bessel functions effectively
USEFUL FOR
Mathematicians, physics students, and engineers dealing with differential equations, particularly those interested in analytical and numerical solutions of Riccati Equations.