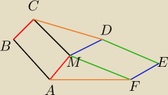
Can Parallelograms Be Constructed in a Convex Hexagon?

[maxkor]

In a convex hexagon $ABCDEF$ exist a point $M$ such that $ABCM$ and $DEFM$ are parallelograms . Prove that exists a point $N$ such that $BCDN$ and $EFAN$ are also parallelograms.

 

[Opalg]

Spoiler

Proof using vectors:

Let $\vec{a},\vec{b},\vec{c},\vec{d},\vec{e},\vec{f},\vec{m}$ be vectors representing the points $A,B.C,D,E,F,M$. Then $\vec{m} = \vec{c} + (\vec{a} - \vec{b})$. Therefore $$\vec{a} + \vec{c} - \vec{b} = \vec{d} + \vec{f} - \vec{e}$$ and so $$\vec{b} + \vec{d} - \vec{c} = \vec{a} + \vec{e} - \vec{f}.$$ Let $N$ be the point given by the vector $$\vec{n} = \vec{b} + \vec{d} - \vec{c}.$$ Then $N$ has the property that $BCDN$ and $EFAN$ are parallelograms.