Schwann
- 7
- 4
Suppose we have a function which looks like this:
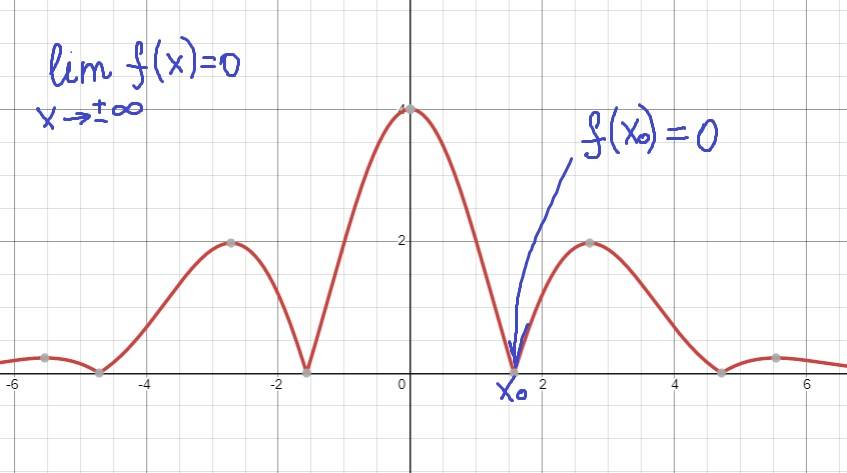
It seems like it meets criteria of probability density functions: this function is asymptotic to zero as x approaches infinity and also it is not negative. My question is: if at some points this function reaches zero (as I have shown above), does that mean that in cannot be PDF?
It seems like it meets criteria of probability density functions: this function is asymptotic to zero as x approaches infinity and also it is not negative. My question is: if at some points this function reaches zero (as I have shown above), does that mean that in cannot be PDF?