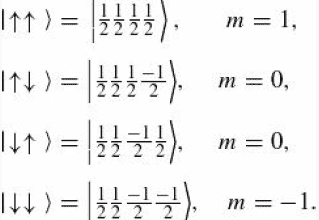SUMMARY
The discussion clarifies the ket notation for spin 1/2 particles, specifically addressing why there are four elements in each ket. Each particle can exhibit two spin states (up or down), leading to four combinations when considering two particles. The notation ##|S_1,S_2,S_{1z},S_{2z}\rangle## is essential for clarity, especially when dealing with spins greater than 1/2. The later editions of Griffiths' Quantum Mechanics simplify this notation by omitting the spin values for compactness.
PREREQUISITES
- Understanding of quantum mechanics principles, particularly spin states.
- Familiarity with ket notation in quantum mechanics.
- Knowledge of Griffiths' Quantum Mechanics, specifically Example 4.5.
- Basic grasp of angular momentum in quantum systems.
NEXT STEPS
- Study Griffiths' Quantum Mechanics, focusing on spin and angular momentum chapters.
- Learn about the implications of spin states in quantum entanglement.
- Explore advanced ket notation for systems with spins greater than 1/2.
- Investigate the mathematical representation of quantum states using Dirac notation.
USEFUL FOR
Students of quantum mechanics, physicists specializing in particle physics, and anyone seeking to deepen their understanding of spin states and ket notation.