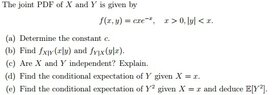nacho-man
- 166
- 0
Please refer to the attached image.
I can't quite get the bounds for question a) right. it's so confusing. Would it be wise to split the double integral into two parts? I guess that's usually favourable with when dealing with absolute values. But the bounds are still confusing me.
would it be easier to integrate with respect to x first, or w.r.t y?For x, it would just be 0 to infinity.
for y it would be -infinity to x ?whilst splitting the integral with respect to x? is this correct.
Actually i'll have a crack at it now. some as i make these question threads i tend to find a solution/or at least get closer to it.
Still, help/correction is very much appreciated.
Thanks!
edit: first attempt i did was
$c \int \int xe^{-x}dxdy = 1$ from $0 \ to \ \infty$ and $-\infty \ to \ x$. this was wrong, as it left me with a variable in my answer, so i will try again but int w.r.t y first.
edit 2: This also did not workedit 3: SOLVED PART A)
i used the bounds -x<y<x and 0<x<infinity
and obtained c= 1/2
edit 4: SOLVED PART B)
I got fy|x(x,y) = $\frac{1}{4x^{3}}$
and fx|y(x,y) = $xe^{-x}$
edit 5: I'm having trouble with part d
E[Y|X=e] = $\int y f_{x|y}(y|x)dy$
I can't quite get the bounds for question a) right. it's so confusing. Would it be wise to split the double integral into two parts? I guess that's usually favourable with when dealing with absolute values. But the bounds are still confusing me.
would it be easier to integrate with respect to x first, or w.r.t y?For x, it would just be 0 to infinity.
for y it would be -infinity to x ?
Actually i'll have a crack at it now. some as i make these question threads i tend to find a solution/or at least get closer to it.
Still, help/correction is very much appreciated.
Thanks!
edit: first attempt i did was
$c \int \int xe^{-x}dxdy = 1$ from $0 \ to \ \infty$ and $-\infty \ to \ x$. this was wrong, as it left me with a variable in my answer, so i will try again but int w.r.t y first.
edit 2: This also did not workedit 3: SOLVED PART A)
i used the bounds -x<y<x and 0<x<infinity
and obtained c= 1/2
edit 4: SOLVED PART B)
I got fy|x(x,y) = $\frac{1}{4x^{3}}$
and fx|y(x,y) = $xe^{-x}$
edit 5: I'm having trouble with part d
E[Y|X=e] = $\int y f_{x|y}(y|x)dy$
Attachments
Last edited: