Change in Gravitational Potential Energy in Oscillating water mass

[Physics2013]

Homework Statement

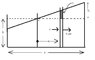
Seiche in a lake. The simplest motion of water in a lake can be approximated as simply the water surface tilting but remaining flat.
Imagine a lake of rectangular cross section of length L and with depth h where (h<<L). The problem resembles that of the simple pendulum, the kinetic energy is due to horizontal
motion and potential energy due to small change in height.
So, imagine at some instant the water level at the increased end is +Y_o with respect to normal level. Show that the increased gravitational potential energy of whole mass system is given by
U=(1/6)bpgL(Yo²)

Homework Equations

U=mgh
Figure attatched!

The Attempt at a Solution

I know the mass of the water will be defined as the volumeXdensity. the volume would be, if width of lake is defined as b, Lbh. Density is denoted p. Thus, m=Lbhp.
The gravitational constant g is applicable so g=g. Finally, as the height is rising as much as it is falling I can take the average height and thus, h = h+(1/2)Y_o?
But, now plugging this into the equation U=mgh I have
U=(Lbhp)g(h+(1/2 Y_o), and this is definitely not the 'answer' stated in the problem.
Could anyone help identify where is my logic going wrong?

 

[hikaru1221]

This one is deadly wrong: h = h+(1/2)Yo (h = h + something?!)
Note that h is the height from the bottom to the average level of the water surface: h = const! What is left is to find the height of the center of mass (COM). Hint: apply the formula of COM's position and express COM's height in term of Yo and D, where D is the height of the left edge of the water surface from the bottom (D is not h!). Then find the geometrical relation between D and Yo.