- #1
xfunctionx
- 9
- 0
Hi, there are a few questions and concepts I am struggling with. The first question comes in 3 parts. The second question is a proof.
Question 1: Please Click on the link below

Question 2: Please Click on the link below
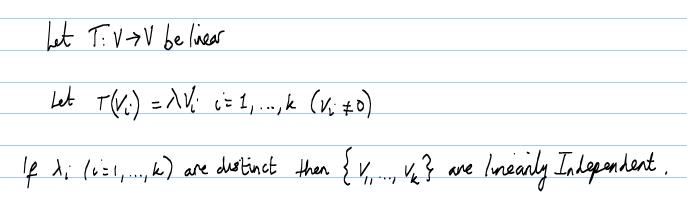
For Q2, could you please show me how to prove this. If possible, could you also link me to a web page where the full proof has already been provided?
I would appreciate the help.
Question 1: Please Click on the link below
Question 2: Please Click on the link below
For Q2, could you please show me how to prove this. If possible, could you also link me to a web page where the full proof has already been provided?
I would appreciate the help.