beans123
- 5
- 0
I'm having trouble understanding how to find out whether or not a stationary point is a minimum and I'm hoping for some clarification. In my class, we were shown that, using Euler's equation, the straight-line path:
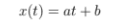
with constants a and b results in a stationary point of the integral:
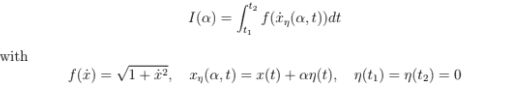
A certain practice question then asks to show that the stationary point corresponds to a minimum. My only attempt so far was performing a simple second derivative test on the function f(x') which turned out to be successful. However, I'm wondering if this is the only way to solve such a problem. I know that a minimum is satisfied if S(a) > S_actual, but can that same idea be mapped onto I(a), that is, is a minimum achieved if I(a) > I_actual (if that even makes sense)? I'm very new to Lagrangian mechanics and find it kind of overwhelming so forgive me if this is a silly question. It just seems that I took the calculus way of solving this when that may not be the ideal method for a class based on Lagrangian mechanics/. I appreciate any help/advice!
with constants a and b results in a stationary point of the integral:
A certain practice question then asks to show that the stationary point corresponds to a minimum. My only attempt so far was performing a simple second derivative test on the function f(x') which turned out to be successful. However, I'm wondering if this is the only way to solve such a problem. I know that a minimum is satisfied if S(a) > S_actual, but can that same idea be mapped onto I(a), that is, is a minimum achieved if I(a) > I_actual (if that even makes sense)? I'm very new to Lagrangian mechanics and find it kind of overwhelming so forgive me if this is a silly question. It just seems that I took the calculus way of solving this when that may not be the ideal method for a class based on Lagrangian mechanics/. I appreciate any help/advice!