- #1
Born
- 31
- 1
Homework Statement
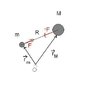
Two particles of mass m and M undergo uniform circular motion about each other at a separation R under the influence of an attractive force F. The angular velocity is ω radians per second. Show that R = (F /w 2 )(1/m + 1/M).(Kleppner & Kollenkow !st ed. problem 2.4)
Homework Equations
$$F=m (or M )ω^2R$$
The Attempt at a Solution
This problem is quite easy to solve using the concept of center of mass. However, the book mentions that until later. How could this be solved just using kinematics and Newton's Laws?
Last edited: