Homework Help Overview
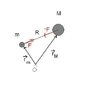
The problem involves two particles of mass m and M undergoing uniform circular motion about each other at a separation R, influenced by an attractive force F and characterized by an angular velocity ω. The task is to demonstrate a relationship involving R, F, m, and M as presented in a textbook problem.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants discuss the use of center of mass concepts versus kinematics and Newton's Laws for solving the problem. Some express confusion about the wording of the problem and its implications for the analysis. Others suggest that the centripetal acceleration is caused by the mutual attraction between the particles, leading to questions about reference frames and fictitious forces.
Discussion Status
The discussion is ongoing, with various interpretations being explored. Some participants have provided insights into the nature of the forces and motions involved, while others are questioning the assumptions made in the problem statement. There is no explicit consensus yet, but several productive lines of reasoning have been suggested.
Contextual Notes
Participants note potential ambiguities in the problem's wording, particularly regarding the description of the motion and the reference frames used for analysis. There is also mention of the need to consider the differing accelerations of the two masses due to their unequal magnitudes.