- #1
Alex126
- 84
- 5
I need help understanding what kind of problem this is at all, since I'm really lost. I'm missing the specific topic name (I called the topic "circular motion" because it's got something to do with it, but maybe it has a more specific sub-topic name), probably missing key formulas, and generally confused by the topic. Up until the point where we did circular motion on a plane it was all clear (the "CD spinning" kind of problems), but this one simply confuses me, I can't understand how to draw forces and stuff.
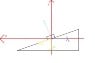
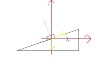
There is an object on a rotating surface (suitcase on a conveyor belt) that forms a known angle ∝ with the horizontal plane (so it's like a rotating cone with something on its surface, somewhere). The surface is rotating. The radius (distance between the object and the "axis" of the cone) r is given.
Another given data is the friction coefficient μ, referring to the friction between the object and the surface.
Not sure if it's of any importance, but the problem specifically mentioned that the object didn't slide all the way down along the rotating surface (it's not at its top, not at its bottom; it's at some unspecified point in-between).
Request: find the time it takes for the object to make a complete lap (full 360° rotation).
In circular motion, T = 2*π/ω (with ω being the angular velocity).
Also, F = m*g for the weight force of an object.
Centripetal Force = m*ω2*r (from F = m*a and a being the centripetal acceleration, which is ω2*r)
Friction Force = μ*Normal force
Normal force on an incline plane of angle α: m*g*cos α
First, I don't know what does friction have to do with the problem. I tried thinking about it, but I don't understand why friction would matter in this case, since the object and the surface (the suitcase and the conveyor belt) are rotating together (so they don't move relatively to each other). The only "use" for friction between them that I can think of is to determine whether the object would slide down or not (thus changing the radius r), and/or whether the object would fly off the surface or not. I wouldn't really know how to verify any of these four possibilities (stay vs slide; stay vs fly off) anyway, but at least they would give significance to the friction coefficient data. If that's not it, then I don't know what to make of it.
I assumed friction was not needed, and tried messing with the equations a bit...and came to the conclusion that I don't have enough equations to solve it. I assume I'm supposed to use T = 2*π/ω, and to find ω from Centripetal Force = m*ω2*r.
I tried googling and searching around, and found this scheme:
https://www.physicsforums.com/attachments/diagram-jpg.4312/
So, from that diagram, F (centripetal force) is also part of that triangle (not sure how that triangle is built though; I guess it comes from the scheme of all the forces, the free-body drawing thing). Therefore from geometry it should be equal to N*sin α
N in its turn should be mg/cos α
So F = mg*sin (α)/cos (α) => F = mg*tan α
From there, F = F =>
m*ω2*r = mg*tan (α)
ω2*r = g*tan (α)
ω = [...]
Tried putting the numbers in there, but the result for T is wrong (not even close).
For the record, I also tried forcing the friction force in there somehow. Assuming that it's got something to do with the horizontal movement, I tried adding or subtracting it (assuming Friction Force = m*g*cosα) to the Centripetal Force. Neither random guess seemed to work.
So...how is this supposed to be done?
Homework Statement
There is an object on a rotating surface (suitcase on a conveyor belt) that forms a known angle ∝ with the horizontal plane (so it's like a rotating cone with something on its surface, somewhere). The surface is rotating. The radius (distance between the object and the "axis" of the cone) r is given.
Another given data is the friction coefficient μ, referring to the friction between the object and the surface.
Not sure if it's of any importance, but the problem specifically mentioned that the object didn't slide all the way down along the rotating surface (it's not at its top, not at its bottom; it's at some unspecified point in-between).
Request: find the time it takes for the object to make a complete lap (full 360° rotation).
Homework Equations
In circular motion, T = 2*π/ω (with ω being the angular velocity).
Also, F = m*g for the weight force of an object.
Centripetal Force = m*ω2*r (from F = m*a and a being the centripetal acceleration, which is ω2*r)
Friction Force = μ*Normal force
Normal force on an incline plane of angle α: m*g*cos α
The Attempt at a Solution
First, I don't know what does friction have to do with the problem. I tried thinking about it, but I don't understand why friction would matter in this case, since the object and the surface (the suitcase and the conveyor belt) are rotating together (so they don't move relatively to each other). The only "use" for friction between them that I can think of is to determine whether the object would slide down or not (thus changing the radius r), and/or whether the object would fly off the surface or not. I wouldn't really know how to verify any of these four possibilities (stay vs slide; stay vs fly off) anyway, but at least they would give significance to the friction coefficient data. If that's not it, then I don't know what to make of it.
I assumed friction was not needed, and tried messing with the equations a bit...and came to the conclusion that I don't have enough equations to solve it. I assume I'm supposed to use T = 2*π/ω, and to find ω from Centripetal Force = m*ω2*r.
I tried googling and searching around, and found this scheme:
https://www.physicsforums.com/attachments/diagram-jpg.4312/
So, from that diagram, F (centripetal force) is also part of that triangle (not sure how that triangle is built though; I guess it comes from the scheme of all the forces, the free-body drawing thing). Therefore from geometry it should be equal to N*sin α
N in its turn should be mg/cos α
So F = mg*sin (α)/cos (α) => F = mg*tan α
From there, F = F =>
m*ω2*r = mg*tan (α)
ω2*r = g*tan (α)
ω = [...]
Tried putting the numbers in there, but the result for T is wrong (not even close).
For the record, I also tried forcing the friction force in there somehow. Assuming that it's got something to do with the horizontal movement, I tried adding or subtracting it (assuming Friction Force = m*g*cosα) to the Centripetal Force. Neither random guess seemed to work.
So...how is this supposed to be done?