Clebsch-Gordan coefficients symmetry relation

[Happiness]

Why are $<j_1j_2m_1m_2|jm>$ and $<j_2j_1m_2m_1|jm>$ negative of each other when $j_1+j_2-j$ is odd as given below?

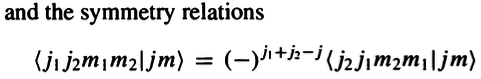
I would expect $<j_1j_2m_1m_2|jm>$ and $<j_2j_1m_2m_1|jm>$ to always have the same sign since nature doesn't care which particle we label as particle 1 and which as particle 2.

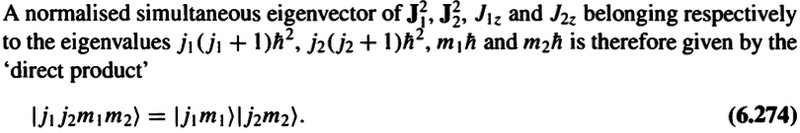
From (6.274), isn't it true that
$|j_1j_2m_1m_2>\,=|j_1m_1>|j_2m_2>\,=|j_2m_2>|j_1m_1>\,=|j_2j_1m_2m_1>$?

And hence
$<j_1j_2m_1m_2|=\,<j_2j_1m_2m_1|$?

And so $<j_1j_2m_1m_2|jm>$ and $<j_2j_1m_2m_1|jm>$ should always have the same sign.

$j$ is the general angular momentum quantum number and $m$ is the associated magnetic quantum number.

 

[Vanadium 50]

Think of a cross product: a x b is - b x a, even though nature doesn't care which particle we call a and which we call b.

 

[Happiness]

Think of a cross product: a x b is - b x a, even though nature doesn't care which particle we call a and which we call b.

Why does the order in the direct product matter?

From (6.276),
$J_z \psi_{j_2 j_1 m_2 m_1}=(m_1+m_2)\hbar\psi_{j_2 j_1 m_2 m_1}$

It seems like the order doesn't matter. Could you give an example where the negative sign is necessary when the order is flipped around?

 

[Vanadium 50]

The important thing the C-G coefficients is their relative sign. That's where the SU(2) algebra is captured. You will need the sign only when you add terms.