Collision Angle for Two Particles with Constant Velocity and Acceleration

[Christoffelsymbol100]

Homework Statement

I am currently solving a problem and I am not sure if it is correct.

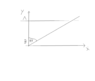
There are two particles A and B. A has a constant velocity with |\vec{v}| = 3 and starts from y = 30

B has constant acceleration with |\vec{a}| = 0,4

The goal is to find the angle between the y-Axis and the path of particle B under which collision with particle A happens.

All I want to know if my result is right, since I am not sure, and if there is another way to solve this

Homework Equations

|\vec{v}| = 3, y = 30
|\vec{a}| = 0,4

The Attempt at a Solution

For particle A and I can say that: \vec{v} = (3,0)

Integrating this with respect to time we get: \vec{x_A} = (3t,0) + (0,30) where the second term represents the starting position

For particle B I can say that: \vec{a} = (sin(\theta),cos(\theta))\cdot 0,4

Integrating this two times with respect to time and setting the starting velocity and starting position as 0 we get: \vec{x_B} = (sin(\theta),cos(\theta))\cdot 0,2 \cdot t^2

Now defining t_C as the time at which the collision happens, the x- and y-components of both x_A and x_B must be the same so:

3\cdot t = sin(\theta) \cdot 0,2 t_C^2 and 30= cos(\theta) \cdot 0,2 t_C^2

From the 1st equation it follows: t_C = \frac{15}{sin(\theta)}

Plugging this into the second equation we will get:

\frac{2}{3} = \frac{cos(\theta)}{sin^2(\theta)}

Solving this for \theta we get: \theta = \frac{\pi}{3} or \theta equals 60 degrees.

 

[DoItForYourself]

Hi,

It seems correct. Good job!

 

[RedDelicious]

You need to rethink your equations for B.

In the x direction, B has no acceleration. Ok. When doing the integrations, you set its initial velocity in both directions to zero as well. Without any acceleration or initial velocity in the x-direction, how do you have it moving in the x-direction?

 

[Christoffelsymbol100]

You need to rethink your equations for B.

In the x direction, B has no acceleration. Ok. When doing the integrations, you set its initial velocity in both directions to zero as well. Without any acceleration or initial velocity in the x-direction, how do you have it moving in the x-direction?

But it has acceleration in the x- and y- direction namely a_x = sin(\theta)*0,4 and a_x = cos(\theta)*0,4. Particle B starts with zero velocity and starts the origin so \vec{x_0} = 0 , \vec{v_0} = 0