Commutation between spin-operator and creation operator(QFT)

[retardedgreensfunc]

TL;DR

Want to find the commutation relation between the z-component spin-operator and creation operator for a transverse polarized photon.

Hi, so I'm currently reading the book "QFT for the gifted amateur", and doing the exercises. In exercise 14.2, which in itself is fine, the authors say that you can show using Noether's theorem that for a transverse polarized photon of momentum q, the z-component of the spin operator obeys the commutation relation:

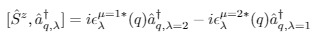
Here, the epsilon is the polariztion vectors, and we assume the photon is traveling in the z-direction.
I really want to be able to derive this for myself, but I have tried for a while now, but without success. Anyone have any tips on how to do this?

 

[vanhees71]

How is $\hat{S}_z$ defined in the book, I don't have at hand right now?

 

[retardedgreensfunc]

How is $\hat{S}_z$ defined in the book, I don't have at hand right now?

I know the mode expansion can be written:

 

[retardedgreensfunc]

Turns out I was overthinking it, and once I had the mode expansion it was very easy to just take the commutator by using the defining commutation relations for the creation and anihilation operators.

 

[vanhees71]

For a photon with $\vec{p}$ in $z$ direction that's the helicity operator (i.e., the projection of the total angular momentum to the direction of the photon momentum). That's the correct polarization quantity for a massless photon. A photon has only two helicity states with eigenvalues $\pm 1$.