Complex Pulley/Force/Circular motion question.

[berkdude022]

Homework Statement

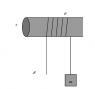
A rope is wrapped through an angle θ about a horizontal pole (So for ex-
ample, θ = 2π would imply the rope goes around one full time). The rope and
the pole have a static friction coeffecient of μ, and the pole is of radius r. From
one end of the rope hangs a mass m. How much force must be exerted on the
other end of the rope to keep the mass from falling?

Homework Equations

F=ma
Fc=mv^2/r

The Attempt at a Solution

So I attempted to draw out FBDs for each section and I got that the string on the left side has a Fpull in the downward direciton, a tension force pulling upward and a friction force upward. On the mass, I have mg pulling down, tension and Fpull in the upward direction.

I have the diagram uploaded.

 

[stockzahn]

This situation has quite a special solution, the formula you need is named after a German scientist: Eytelwein. I don't know if your task is to derive the formula by yourself, but this wouldn't be very easy. If you want to try it you have to draw the FBD for a small piece of rope (for a small angle dθ).