Conceptual question about frictional force and equilibrium

[lichenguy]

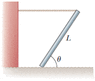
A uniform beam of length L and mass m is inclined at an angle θ to the horizontal. Its upper end
is connected to a wall by a rope, and its lower end rests on a rough, horizontal
surface. The coefficient of static friction between the beam and surface is μ_s.
Assume that the angle θ is such that the friction force is at its maximum value.
a) Draw a force diagram for the beam.
b) Using the condition of rotational equilibrium, find an expression for the tension T in the rope in terms of m, g and θ.
c) obtain an expression for μ_s, involving only the angle θ.

e) What happens if the ladder is lifted upward and its base is placed back on the ground slightly to the left of its former position? Explain.

I did a, b, and c, but I'm not sure on e. The graph shows μ in terms of the angle θ.

For e i wrote, so far, that F_N would decrease because F_T would now have a component in the same direction as F_N.
If I'm understanding this right, μ_s is changing to maintain the equilibrium?

Also, I'm not sure what is meant by "Assume that the angle θ is such that the friction force is at its maximum value.".

 

[haruspex]

FT would now have a component in the same direction as FN.

True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in F_T is of the order x², so I think you are supposed to ignore that.

Assume that the angle θ is such that the friction force is at its maximum value.".

As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.

 

[lichenguy]

True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in F_T is of the order x², so I think you are supposed to ignore that.

As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.

Ok, ty, i get the maximum frictional force thing now.

On the e question, pulling it back will decrease the angle, but am guessing it won't change the angle in the same way as before? Before we moved the top, not the bottom.

 

[lichenguy]

True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in F_T is of the order x², so I think you are supposed to ignore that.

As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.

Does it depend on the length of the ladder? Because i found something, but I'm not sure if it's right.

 

[haruspex]

Does it depend on the length of the ladder? Because i found something, but I'm not sure if it's right.

It's a qualitative question. No, the length of the ladder does not matter.
If the base is shifted to the left, what will happen to the frictional force that is needed to maintain equilibrium? Will it increase, decrease or stay the same?

 

[lichenguy]

It's a qualitative question. No, the length of the ladder does not matter.
If the base is shifted to the left, what will happen to the frictional force that is needed to maintain equilibrium? Will it increase, decrease or stay the same?

There will be need for an increased frictional force to stay up. If the frictional force doesn't increase it will fall over, i guess.

I tried to find out if the rate of change of μ that we found earlier was enough to maintain equilibrium while moving the base back. I guess that's not what was asked.

 

[haruspex]

If the frictional force doesn't increase it will fall over,

Yes, but it is a bit inaccurate to say it will fall over. The base might hit the wall first. Just say the ladder will slip, and give your reason.

 

[lichenguy]

Yes, but it is a bit inaccurate to say it will fall over. The base might hit the wall first. Just say the ladder will slip, and give your reason.

Alright :D i didn't think of it hitting the wall, hehe.
Thanks lad!

 

[CWatters]

There will be need for an increased frictional force to stay up. If the frictional force doesn't increase it will fall over, i guess.

Assuming the surface is uniform, what affects the available friction force? Does that increase or decrease if the base is shifted to the left?