Guillem_dlc
- 188
- 17
- Homework Statement
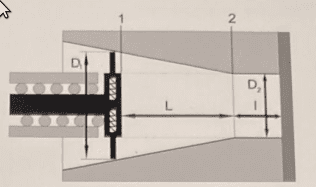
- The device shown in figure 1 is a compressor driven by an electromagnet. When the piston is in position 1 it sucks in nitrogen at ##p_1=101300\, \textrm{Pa}## and ##T_1=20\, \textrm{ºC}##.
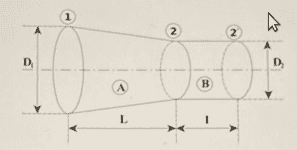
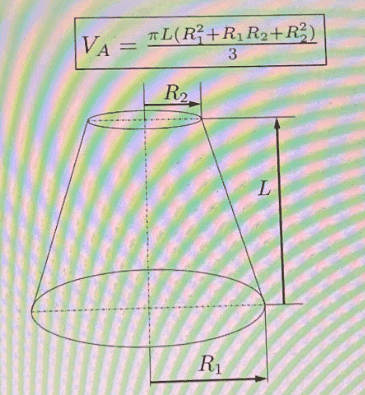
Determine what is the pressure, at ##\textrm{kPa}##, when the piston reaches position 2 and the gas exits through the exhaust valve, assuming the process is isothermal (the valves are not represented in the figure). Other data: ##\bar{M}_N=28\, \textrm{kg}/\textrm{kmol}##; ##R=8314\, \textrm{J}/(\textrm{kmolK})##; ##D_1=35\, \textrm{mm}##; ##D_2=20\, \textrm{mm}##; ##L=40\, \textrm{mm}##; ##l=15\, \textrm{mm}##. See also the other figures. The second figure represents the stroke volume ##V_A## and the exhaust volume ##V_B##. And the third figure represents the volume of a truncated cone.
Solution: ##p_2=261,692\, \textrm{kPa}##
- Relevant Equations
- Volumes formulas, ##\rho =\dfrac{p}{R^2T}##
Figures:
Attempt at a Solution:
$$L=0,015\, \textrm{m}\qquad R_2=0,01\, \textrm{m}$$
$$R_1-R_2=R_D=0,0075\, \textrm{m}$$
$$L=0,04$$
$$\rho_1=\dfrac{p_1}{R^2T_1}=\dfrac{p_1\bar{M}}{RT_1}=1,164\, \textrm{kg}/\textrm{m}^3$$
Calculate total volume ##V_A+V_B##:
$$V_B=\pi \cdot R_2^2\cdot L=4,712\cdot 10^{-6}\, \textrm{m}^3$$
$$V_A=\dfrac{\pi L(R_1^2+R_1R_2+R_2^2)}{3}=24,347\cdot 10^{-6}\, \textrm{m}^3$$
$$\rightarrow m=\rho_1 (V_A+V_B)$$
The piston then reaches position 2.
$$\rho_2=\dfrac{m}{V_B}=\dfrac{\rho_1 (V_A+V_B)}{V_B}=7,178\, \textrm{kg}/\textrm{m}^3$$I have done this and I don't know how to continue.
Attempt at a Solution:
$$L=0,015\, \textrm{m}\qquad R_2=0,01\, \textrm{m}$$
$$R_1-R_2=R_D=0,0075\, \textrm{m}$$
$$L=0,04$$
$$\rho_1=\dfrac{p_1}{R^2T_1}=\dfrac{p_1\bar{M}}{RT_1}=1,164\, \textrm{kg}/\textrm{m}^3$$
Calculate total volume ##V_A+V_B##:
$$V_B=\pi \cdot R_2^2\cdot L=4,712\cdot 10^{-6}\, \textrm{m}^3$$
$$V_A=\dfrac{\pi L(R_1^2+R_1R_2+R_2^2)}{3}=24,347\cdot 10^{-6}\, \textrm{m}^3$$
$$\rightarrow m=\rho_1 (V_A+V_B)$$
The piston then reaches position 2.
$$\rho_2=\dfrac{m}{V_B}=\dfrac{\rho_1 (V_A+V_B)}{V_B}=7,178\, \textrm{kg}/\textrm{m}^3$$I have done this and I don't know how to continue.