Conceptual question - block and incline

[deedsy]

Homework Statement

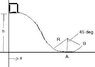
a block of mass m = 1.62kg slides down a frictionless incline.the block is raised a height h = 3.91m above the bottom of theloop.
(a) what is the force of the inclined track on the block atthe bottom (point A)?
(b) what is the force of the track on the block at pointB?
(c) at what speed does the block leave the track?
(d) how far way from point A does the block land on levelground?
(e) sketch the potential energy U(x) of the block. indicatethe total energy on the sketch

Homework Equations

The Attempt at a Solution

I know how to work out this problem, but I don't understand why the force of the inclined track on the block at the bottom depends on air resistance. At the flat, bottom, the force diagram should just conclude N=mg, but I'm told there is a retarding force dependent on v as well. This retarding force seems like it should be to the left, and would have no relation to the normal force.

 

[gneill]

? The problem states that the track is frictionless, and there is no mention made of air resistance...

Looks like you'll just have the forces due to gravity and inertial forces due to motion to deal with (pay attention to the geometry of the lower portion of the track).

 

[deedsy]

? The problem states that the track is frictionless, and there is no mention made of air resistance...

Looks like you'll just have the forces due to gravity and inertial forces due to motion to deal with (pay attention to the geometry of the lower portion of the track).

So should the answer to part A simply be m*g? Or is there a component of the inertial force in the y-direction too?

 

[gneill]

So should the answer to part A simply be m*g? Or is there a component of the inertial force in the y-direction too?

What might be a cause of an inertial force acting at A? Hint: the answer for (a) is not just m*g.

 

[deedsy]

What might be a cause of an inertial force acting at A? Hint: the answer for (a) is not just m*g.

ooo is it the centripetal force?

So at point A, N - mg = mv^2/r

Thank you very much for helping me

 

[gneill]

ooo is it the centripetal force?

So at point A, N = mg + mv^2/r

or is it mg - mv^2/r since the force is directed towards the center of the circle like the normal force

Yes, centripetal force. Regarding the direction, the centripetal force is acting in the same direction as the normal force, and it's the normal force that you're looking for, right? (check the question statement). The track has to provide the centripetal force IN ADDITION to supporting the block's gravitational weight...

 

[skeer]

Is there a way to find the numerical value of R?

 

[gneill]

Is there a way to find the numerical value of R?

If it's not explicitly given (and it is not), and if there is not some related value from which we could deduce it (and there is not) then no, we can't find a numerical value for R