Conflicting Conventions for Bernoulli Numbers?

[nomadreid]

TL;DR

In the Wiki article on Bernoulli numbers, it gives two expressions that, if I understand correctly, are supposed to be equal except at one point. But I am not sure I understand it correctly

In the Wikipedia article https://en.wikipedia.org/wiki/Bernoulli_number on Bernoulli’s numbers, it explains that there are two conventions which differ only at m=1. Then it says…

Under “explicit definitions”, it gives, for m>1

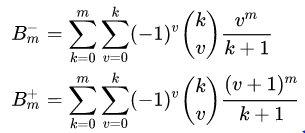
So, it seems pretty straightforward that they are saying that (except for m=1) these two expressions are equal, but that all the extra terms in the second expression (+) not included in the first one (-) would cancel out seems so incredible that I think I might be misinterpreting something. Am I?

Thanks

 

[DrClaude]

The expansion of $(v+1)^m$ follows Pascal's triangle, hence binomial coefficients, so yes, the terms can cancel out.

 

[nomadreid]

Thanks, DrClaude