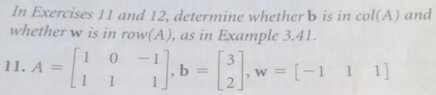Discussion Overview
The discussion revolves around Exercise 11 from a textbook, where participants express confusion regarding the answer key's claims about the inclusion of vectors b and w in the column space of matrix A. The conversation includes attempts to clarify the problem, share solutions, and address potential errors in the answer key.
Discussion Character
- Debate/contested
- Mathematical reasoning
- Homework-related
Main Points Raised
- One participant initially claims that vector b is not in the column space of A while w is, contradicting the answer key which states that b is in and w is not.
- Another participant suggests that sharing the solution could help clarify the misunderstanding.
- There are multiple references to the term "facit," which is clarified to mean the answer key, with some participants expressing confusion about its correctness.
- A participant provides a row-reduced form of the matrix and concludes that there are infinitely many solutions, suggesting that b is indeed in col(A).
- One participant acknowledges a mistake in their matrix calculations, leading to a revised understanding of the problem.
- Another participant presents a mathematical argument to show that b is in col(A) through a specific linear combination.
- A philosophical point is raised about the nature of answer keys, arguing that they can be misleading and that understanding the reasoning behind answers is more important than simply obtaining them.
Areas of Agreement / Disagreement
Participants express disagreement regarding the status of vectors b and w in relation to the column space of A, with no consensus reached on the correctness of the answer key. Some participants revise their positions based on further analysis, while others maintain differing views.
Contextual Notes
There are unresolved issues regarding the accuracy of the answer key and the participants' interpretations of the exercise, as well as potential errors in calculations that have not been fully clarified.