kelly0303
- 573
- 33
Hello! I am trying to simulate the following experiment. It is a counting experiment where the probability of getting an event after a given trial is given by:
$$P = 2\left(\frac{a}{x}+\frac{b}{c}\right)^2\left(1-\cos\left(\frac{\pi x}{x_0}\right)\right)$$
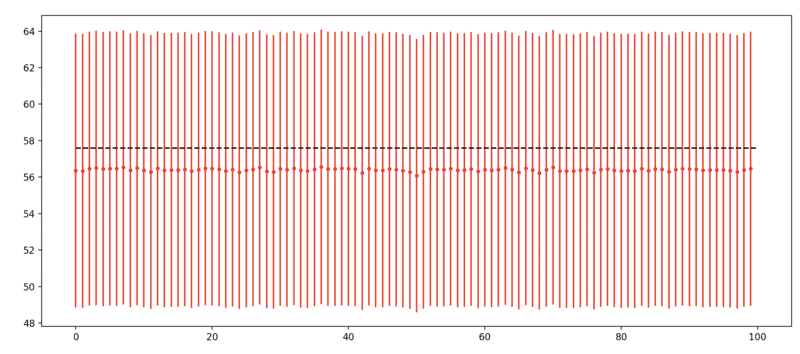
where, ##a = 4\pi##, ##b = 2000\pi##, ##c = 20000\pi## and ##x_0 = 200\pi## are fixed parameters (we can assume there is no uncertainty on them), and ##x## is an experimental parameter whose value from one measurement instance to the next changes based on a gaussian with mean ##200\pi## and standard deviation ##20\pi##. In my case this probability is about ##0.058##. In my simulations I sample ##x## 1000 times and compute P for each of these, then I sum up all the P values, which is basically the number of events I would see in the experiment (0.058 probability x 1000 experiments ~ 58 measured event), call it N. The uncertainty on N, in my simulations, I assume to be ##\sqrt{N}##. I do this 100 times and in the end I get the plot attached below, showing the number of counts for each of the 100 simulations. The black line is the expected number of counts for ##x = x_0##. I am confused about the fact that I am constantly under-estimating the true value and by the fact that I am so much closer to the true value than expected from the errors. Can someone help me understand what am I doing wrong? Thank you!
$$P = 2\left(\frac{a}{x}+\frac{b}{c}\right)^2\left(1-\cos\left(\frac{\pi x}{x_0}\right)\right)$$
where, ##a = 4\pi##, ##b = 2000\pi##, ##c = 20000\pi## and ##x_0 = 200\pi## are fixed parameters (we can assume there is no uncertainty on them), and ##x## is an experimental parameter whose value from one measurement instance to the next changes based on a gaussian with mean ##200\pi## and standard deviation ##20\pi##. In my case this probability is about ##0.058##. In my simulations I sample ##x## 1000 times and compute P for each of these, then I sum up all the P values, which is basically the number of events I would see in the experiment (0.058 probability x 1000 experiments ~ 58 measured event), call it N. The uncertainty on N, in my simulations, I assume to be ##\sqrt{N}##. I do this 100 times and in the end I get the plot attached below, showing the number of counts for each of the 100 simulations. The black line is the expected number of counts for ##x = x_0##. I am confused about the fact that I am constantly under-estimating the true value and by the fact that I am so much closer to the true value than expected from the errors. Can someone help me understand what am I doing wrong? Thank you!