LaTeX Congratulations latex a plot question

[leprofece]

First of all I see we have an editor latex so my friend markflo I won't have morre problems
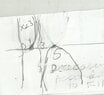
But my problem is about a graph
Plot a continue function graph with the following data o properties
f(1)= 0
f of first derivative in (3) = \infty
f of first derivative in (5) = 0
first derivative (x) > 0 in x <3 and x > 5
first derivative (x) < 0 in 3<x<5
second derivative (x) > 0 in - in \infty<x<+\inftyI got The plot in the image shown
an asintote in 3 and go to \infty in both sides left to 3 and right to 3 View attachment 2679

Am I right?? anything wrong in my plot ?

 

[Opalg]

f(1)= 0 Yes
f of first derivative in (3) = \infty Yes: you have shown f going to $\color{red}{-\infty}$ on both sides at $\color{red}{x=3}$. You should consider whether that should be $\color{red}{+\infty}$ on one or both sides.
f of first derivative in (5) = 0 No: you have shown the function being zero at 5. It should be the first derivative that vanishes, not the function.
first derivative (x) > 0 in x <3 and x > 5 No: your function is decreasing when $\color{red}{x<3}$. It should be increasing, if the first derivative is positive.
first derivative (x) < 0 in 3<x<5 No: your function is increasing when $\color{red}{3<x<5}$. It should be decreasing.
second derivative (x) > 0 in - in \infty<x<+\infty This means that the first derivative should always be increasing. In the graph, that means that the curve should always be bending to the left as $\color{red}{x}$ increases.

 

[leprofece]

f(1)= 0 Yes
f of first derivative in (3) = \infty Yes: you have shown f going to $\color{red}{-\infty}$ on both sides at $\color{red}{x=3}$. You should consider whether that should be $\color{red}{+\infty}$ on one or both sides.
f of first derivative in (5) = 0 No: you have shown the function being zero at 5. It should be the first derivative that vanishes, not the function.
first derivative (x) > 0 in x <3 and x > 5 No: your function is decreasing when $\color{red}{x<3}$. It should be increasing, if the first derivative is positive.
first derivative (x) < 0 in 3<x<5 No: your function is increasing when $\color{red}{3<x<5}$. It should be decreasing.
second derivative (x) > 0 in - in \infty<x<+\infty This means that the first derivative should always be increasing. In the graph, that means that the curve should always be bending to the left as $\color{red}{x}$ increases.

could you please send me your graph ?''
is it the contrary to mine ?? I mean at 5 up and 1 too
Something like that? View attachment 2680

 

[MarkFL]

Let's look at your latest plot...can you say that:

$$\lim_{x\to3^{-}}f'(x)=\lim_{x\to3^{+}}f'(x)=+\infty$$ ?

 

[Opalg]

The second sketch is much better. The only thing wrong with it is that it still shows $f(5)=0$. What you are told is that the first derivative is zero at $x=5$. This means that the curve should have a horizontal tangent when $x=5$. When $x>5$ the first derivative should be positive, which means that the function should be increasing.

 

[MarkFL]

The second sketch is much better. The only thing wrong with it is that it still shows $f(5)=0$. What you are told is that the first derivative is zero at $x=5$. This means that the curve should have a horizontal tangent when $x=5$. When $x>5$ the first derivative should be positive, which means that the function should be increasing.

Perhaps I am misunderstanding, but isn't there still a problem at the vertical asymptote? :D

 

[Opalg]

Perhaps I am misunderstanding, but isn't there still a problem at the vertical asymptote? :D

I don't think so. The conditions say that the derivative should be positive for $x<3$ and negative for $3<x<5$. That seems to mean that the graph must go up to $+\infty$ and then come down from $+\infty$. Also, the second derivative condition implies that the graph must always have a leftward turn to it as you travel along the curve.

 

[MarkFL]

I don't think so. The conditions say that the derivative should be positive for $x<3$ and negative for $3<x<5$. That seems to mean that the graph must go up to $+\infty$ and then come down from $+\infty$. Also, the second derivative condition implies that the graph must always have a leftward turn to it as you travel along the curve.

I see...I looked only at the first statement:

"f of first derivative in (3) = \infty "

I took this to mean that the slope is positive in the neighborhood of $x=3$, that is, the function is increasing on either side of a vertical asymptote. :D

 

[leprofece]

In conclusion What should the right sketh be??

 

[MarkFL]

In conclusion What should the right sketh be??

Read Opalg's post (post #5). What should be going on at $x=5$?

 

[leprofece]

Read Opalg's post (post #5). What should be going on at $x=5$?

OK WHAT IS CORRECT PLOT 1 or PLOT 2? Thanks
Ithink is plot 1 but since I have un min in 5 I got a parabole in plot 2 with a vertex in 5?

 

[MarkFL]

OK WHAT IS CORRECT PLOT 1 or PLOT 2? Thanks
Ithink is plot 1 but since I have un min in 5 I got a parabole in plot 2 with a vertex in 5?

Neither plot is correct, but your second plot is closer to being correct. Yes, you should have a local minimum at $x=5$, but this does not mean you have to have a parabolic curve. Read Opalg's first post carefully...he gives you many points to consider.

 

[leprofece]

View attachment 2684

Neither plot is correct, but your second plot is closer to being correct. Yes, you should have a local minimum at $x=5$, but this does not mean you have to have a parabolic curve. Read Opalg's first post carefully...he gives you many points to consider.

This plot has the same as 1st post of opalg the thing is that he says in the last part of the post that graph is always increasing but in 3<x<5 he also says that it is decreasing
View attachment 2684

 

[MarkFL]

You are still insisting on using $f(5)=0$ rather than $f'(5)=0$. You should have a local minimum at $x=5$. The function should be decreasing for $3<x<5$ too, right?

 

[leprofece]

OHHH MY GOD! So parabole down with vertex in 5? if no I don't try any more
View attachment 2686

 

[MarkFL]

You do now indicate an extremum at $x=5$, but it is a local maximum. Your function needs to decreases on $3<x<5$ and then increase on $5<x$. This means you need a local minimum at $x=5$.

Please don't give up...it is vital that you understand how to do this problem correctly, otherwise you will encounter difficulties in similar problems and as you progress in your study of calculus.

Let's look at this problem one step at a time...

a) You are told $f(1)=0$. You have this done correctly.

b) You are told that there is a vertical asymptote at $x=3$. You have this done correctly.

c) You are told $f'(5)=0$. You have this done correctly.

d) You are told that $0<f'(x)$ for $x<3$. You have this done correctly.

e) You are told that $0<f'(x)$ for $5<x$. You have NOT done this correctly in your latest plot. You have $f$ decreasing now on this interval.

f) You are told $0<f''(x)$ for all $x$ in the domain. This means the function should be "concave up," yet you have $f$ being concave down on $3<x$.

So, you only need change what you have to the right of $x=3$. You want the function to come down from the vertical asymptote at $x=3$, reach a turning point at $x=5$ (the actual vaule of $f(5)$ doesn't matter), and then increase at an increasing rate to the right of $x=5$.

 

[leprofece]

Something like that?View attachment 2687

 

[MarkFL]

It looks like you've simply gone back to your previous plot. :(

 

[leprofece]

According your last post that is how i Understood it

 

[MarkFL]

Your plot is not decreasing on $3<x<5$...

 

[leprofece]

to do that it is as i put in plot 2 before
I DID IT in all the ways and all of them are wrong I don't know how to do it in another way

 

[MarkFL]

Yes, but plot 2 has the function decreasing on $3<x$, not just on $3<x<5$.

 

[Opalg]

Can you see why something like this satisfies all the conditions of the problem?

[graph]f2xbdnp95p[/graph]