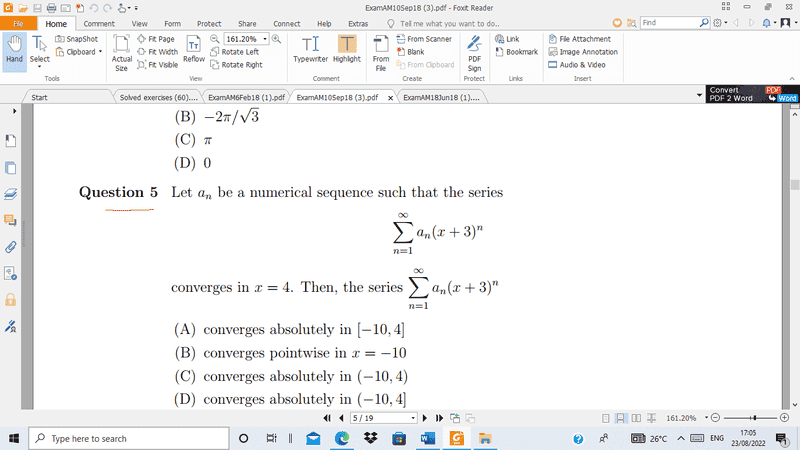SUMMARY
The discussion centers on the convergence of a series defined by the transformation y = x + 3, with a focus on the radius and set of convergence. Participants clarify that the phrase "converges in x=4" should be interpreted as "converges at x=4," indicating that the series converges at the boundary defined by the interval -1 < y < 7. The radius of convergence is centered at y=0, not at x=3, and the width of the interval of convergence is twice the radius. The correct interpretation of convergence terminology is crucial for determining the accurate endpoints of the region of convergence.
PREREQUISITES
- Understanding of power series and their convergence properties
- Familiarity with the concept of radius of convergence
- Knowledge of interval notation and its application in mathematical analysis
- Basic algebraic manipulation involving transformations of variables
NEXT STEPS
- Study the definition and calculation of the radius of convergence for power series
- Learn about absolute versus conditional convergence in series
- Explore the implications of endpoint behavior in convergence intervals
- Review examples of series convergence and the application of transformations like y = x + 3
USEFUL FOR
Students and educators in mathematics, particularly those studying calculus and series convergence, as well as anyone involved in mathematical analysis and problem-solving related to power series.