MHB Convert 7sqrt5 cis(tan−1 (2)) to Rectangular Form - Yahoo! Answers

[MarkFL]

Here is the question:

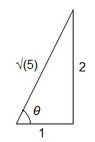
Express in the form a + bi, where a and b are real numbers.?

7sqrt5 cis(tan−1 (2))

Here is a link to the question:

Express in the form a + bi, where a and b are real numbers.? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello Meredith,

We are given:

$$z=7\sqrt{5}\text{cis}\left(\tan^{-1}(2) \right)=7\sqrt{5}\left(\cos\left(\tan^{-1}(2) \right)+i\sin\left(\tan^{-1}(2) \right) \right)$$

In order to evaluate the trig functions, consider the following diagram:

https://www.physicsforums.com/attachments/782._xfImport

As you can see:

$$\tan(\theta)=\frac{2}{1}=2\,\therefore\,\theta= \tan^{-1}(2)$$

and so:

$$\sin(\theta)=\frac{2}{\sqrt{5}}$$

$$\cos(\theta)=\frac{1}{\sqrt{5}}$$

and so we have:

$$z=7\sqrt{5}\left(\frac{1}{\sqrt{5}}+i\frac{2}{ \sqrt{5}} \right)=7+14i$$

Hence:

$$a=7,\,b=14$$

To Meredith and any other guests viewing this topic, I invite and encourage you to post other complex number problems in our http://www.mathhelpboards.com/f21/ forum.

Best Regards,

Mark.