Cost of the conversion of a string to an other string

[evinda]

Hello! (Wave)

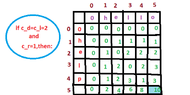
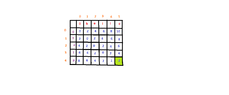
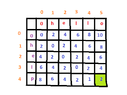
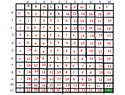
We are given $2$ strings $A=[1 \dots m]$ and $B[1 \dots n]$ and the following $3$ operations are allowed:

• Insert a charachter,with cost $c_i$
• Delete a character,with cost $c_d$
• Replace a character,with cost $c_r$

We are looking for the optimal sequence of operations(sequence of operations with the minimum cost),for the conversion of the string $A$ to the string $B$.

$$T(i,j)=\text{ the minimum cost of the conversion of the string } A[1 \dots i] \text{ to } B[1 \dots j], 1 \leq i \leq m, 1 \leq j \leq n$$

According to my notes:
$$T(i,j)=\min \left\{\begin{matrix}
T(i-1,j)+c_d & \text{ // delete the i-th charachter of A}\\
T(i,j-1)+c_i & \text{ // insert the j-th charachter of B} \\
T(i-1,j-1) & \text{if } A=B[j]\\
T(i-1,j-1)+c_r & \text{if } A \neq B[j]
\end{matrix}\right.$$

Why is the cost given by the above formula?Could you explain it to me? (Thinking)

 

[Evgeny.Makarov]

The $\le$ direction is pretty obvious since the right-hand side suggests recursive algorithms to do the conversion.

 

[I like Serena]

Let's pick an example.
Suppose you want to transform A="help" to B="hello".
How would you do it?
Which other alternatives do you have?

 

[evinda]

Let's pick an example.
Suppose you want to transform A="help" to B="hello".
How would you do it?
Which other alternatives do you have?

That's what I have tried:

View attachment 2993

Is it right? If so,is the cost $T[5,5]=10$?Or don't we have to take $T[n,n]$ as the minimum cost of the conversion? (Thinking)

 

[I like Serena]

That's what I have tried:

Is it right? If so,is the cost $T[5,5]=10$?Or don't we have to take $T[n,n]$ as the minimum cost of the conversion? (Thinking)

I don't quite understand your table.
Can you explain? (Wondering)Anyway, the most obvious ways I can think of are:

1. Keep "hel".
2. Replace 'p' by 'l'.
3. Insert 'o' at the end.

With your costs, that gives us a cost of 1+2=3.

Alternatively, we could do:

1. Keep "hel".
2. Insert 'l'.
3. Replace 'p' by 'o'.

With your costs, that gives us a cost of 2+1=3.

As another alternative, we could do:

1. Keep "hel".
2. Delete 'p'.
3. Insert 'l' at the end.
4. Insert 'o' at the end.

With your costs, that gives us a cost of 2+2+2=6.

So the first 2 methods are cheaper than the last.
And I have left out a whole bunch of alternatives that will be more expensive.

In all cases presented T(3,3)=0.
In the first method, we would get T(4,4)=1 and T(4,5)=3.
In the last method, we would get T(3,4)=2, T(4,4)=4, and T(4,5)=6.
Taking the minimum recursively from the end should lead us to the cheapest solution.

 

[evinda]

I don't quite understand your table.
Can you explain? (Wondering)Anyway, the most obvious ways I can think of are:

1. Keep "hel".
2. Replace 'p' by 'l'.
3. Insert 'o' at the end.

With your costs, that gives us a cost of 1+2=3.

Alternatively, we could do:

1. Keep "hel".
2. Insert 'l'.
3. Replace 'p' by 'o'.

With your costs, that gives us a cost of 2+1=3.

As another alternative, we could do:

1. Keep "hel".
2. Delete 'p'.
3. Insert 'l' at the end.
4. Insert 'o' at the end.

With your costs, that gives us a cost of 2+2+2=6.

So the first 2 methods are cheaper than the last.
And I have left out a whole bunch of alternatives that will be more expensive.

In all cases presented T(3,3)=0.
In the first method, we would get T(4,4)=1 and T(4,5)=3.
In the last method, we would get T(3,4)=2, T(4,4)=4, and T(4,5)=6.
Taking the minimum recursively from the end should lead us to the cheapest solution.

I understand... I tried to create a matrix for $T[i,j]$ using the formula:

$$T(i,j)=\min \left\{\begin{matrix}
T(i-1,j)+c_d & \text{ // delete the i-th charachter of A}\\
T(i,j-1)+c_i & \text{ // insert the j-th charachter of B} \\
T(i-1,j-1) & \text{if } A=B[j]\\
T(i-1,j-1)+c_r & \text{if } A \neq B[j]
\end{matrix}\right.$$

but there is no cost,if we don't make any changes at a position,right? So, the cost doesn't increase , when we keep "hel" ..Or have I understood it wrong? (Thinking)

 

[I like Serena]

I understand... I tried to create a matrix for $T[i,j]$ using the formula:

$$T(i,j)=\min \left\{\begin{matrix}
T(i-1,j)+c_d & \text{ // delete the i-th charachter of A}\\
T(i,j-1)+c_i & \text{ // insert the j-th charachter of B} \\
T(i-1,j-1) & \text{if } A=B[j]\\
T(i-1,j-1)+c_r & \text{if } A \neq B[j]
\end{matrix}\right.$$

but there is no cost,if we don't make any changes at a position,right? So, the cost doesn't increase , when we keep "hel" ..Or have I understood it wrong? (Thinking)

You have understood it right. Keeping "hel" does not incur any cost. (Nod)

So let's take a look at your table.
We start with T(0,0) which is indeed 0, since nothing is done.
Looking at T(0,1) means we have inserted character 1 of B into A with the cost of 2.
So I think T(0,1) should be 2... (Thinking)

I see you do have T(3,3)=0, T(4,4)=1, T(4,5)=3.
I think the total cost would be T(4,5)=3, since A has 4 characters and B has 5 characters.

 

[evinda]

So let's take a look at your table.
We start with T(0,0) which is indeed 0, since nothing is done.
Looking at T(1,0) means we have inserted character 1 of B into A with the cost of 2.
So I think T(1,0) should be 2... (Thinking)

So,isn't it $T(i,j)=0 \text{ if } i=0 \text{ or } j=0$ ? (Thinking)

At the position $0$,there is no letter , or am I wrong? (Sweating)

 

[I like Serena]

So,isn't it $T(i,j)=0 \text{ if } i=0 \text{ or } j=0$ ? (Thinking)

At the position $0$,there is no letter , or am I wrong? (Sweating)

Isn't T(0,1) the mimimum cost to transform the string of length 0 ("") to the string of length 1 ("h")? (Wondering)
That would mean that we need to insert 'h' for a cost of $c_i$.

 

[evinda]

Isn't T(0,1) the mimimum cost to transform the string of length 0 ("") to the string of length 1 ("h")? (Wondering)
That would mean that we need to insert 'h' for a cost of $c_i$.

I tried it again..Tha's what I did:

View attachment 3001

Is it right now or have I done something wrong? (Thinking)

 

[I like Serena]

I think the final T(4,5) value should be 3... (Worried)

 

[evinda]

I think the final T(4,5) value should be 3... (Worried)

Because of the fact that we have to insert o and replace p by l,right? (Thinking)

 

[I like Serena]

Because of the fact that we have to insert o and replace p by l,right? (Thinking)

Yes. Actually we have 2 paths to the same result.
Either we replace first and insert afterwards.
Or we insert first and replace afterwards.
Both of them add up to 3. (Nerd)

 

[evinda]

Yes. Actually we have 2 paths to the same result.
Either we replace first and insert afterwards.
Or we insert first and replace afterwards.
Both of them add up to 3. (Nerd)

A ok..I understand! (Nod)
But..what do we have to do in this case:

View attachment 3002

to find,for example $T(3,2)$ and $T(3,3)$ ? For $T(3,2)$ we have to delete one letter,for $T(3,3)$ we don't have to insert a letter and also not to delete one..

For $T(3,2)$,do we have to replace two letters?Or not,since we already have a $p$ ?

Also,for $T(3,3)$ do we have to replace all the three letters,so the minimum cost is $3$ ? (Thinking)

 

[I like Serena]

A ok..I understand! (Nod)
But..what do we have to do in this case:

to find,for example $T(3,2)$ and $T(3,3)$ ? For $T(3,2)$ we have to delete one letter,for $T(3,3)$ we don't have to insert a letter and also not to delete one..

True. (Nod)

For $T(3,2)$,do we have to replace two letters?Or not,since we already have a $p$ ?

To find $T(3,2)$ we need to find the cheapest way, choosing from $T(2,1)$, $T(2,2)$, and $T(3,1)$.
As it is, replace-replace-delete (4) is cheaper than delete-delete-insert (6).
So yes, we have to replace two letters, and we can't make effective use of the existing 'p' (yet). (Happy)

Also,for $T(3,3)$ do we have to replace all the three letters,so the minimum cost is $3$ ? (Thinking)

Yep!

 

[evinda]

To find $T(3,2)$ we need to find the cheapest way, choosing from $T(2,1)$, $T(2,2)$, and $T(3,1)$.
As it is, replace-replace-delete (4) is cheaper than delete-delete-insert (6).
So yes, we have to replace two letters, and we can't make effective use of the existing 'p' (yet). (Happy)

I understand! (Smile)

I tried to find the cost,in this case :

View attachment 3006

Could you tell me if it is right or if I have done something wrong? (Thinking)
Is the cost $T(11,10)=9$ ? (Thinking)

 

[I like Serena]

I've started with the path where we simply replace all characters and finally delete the last.
In T(5,5) we have indeed 4 replacements.
How did you get T(6,6)=6?
Shouldn't it be 5? (Wondering)As for your final T(11,10)=9, shouldn't it be at least as high as the lowest of the 3 squares left and above? (Wondering)The last 3 letters "ial" are identical.
So I would expect they could remain the same without cost, but in your table the cost seems to go up as if they were replaced. (Worried)

 

[evinda]

How did you get T(6,6)=6?
Shouldn't it be 5? (Wondering)

Why should it be T(6,6)=5? (Thinking)
Don't we have two replace all the 6 letters e,x,p,o,n,e by these ones: p,o,l,y,n,o ?
If we would keep "po" and "n",wouldn't it be like that:

delete e,x -> cost=4
keep po-> cost=0
insert l,y-> cost=4
keep n-> cost=0
replace e by o-> cost=1

So,wouldn't the cost be $9$ ?

Or have I done somrthing wrong?

As for your final T(11,10)=9, shouldn't it be at least as high as the lowest of the 3 squares left and above? (Wondering)The last 3 letters "ial" are identifical.
So I would expect they could remain the same without cost, but in your table the cost seems to go up as if they were replaced. (Worried)

Oh yes,you are right! (Nod)

So..to calculate T(11,10) , do we have to do the following?

replace all the letters from e till o,keep "n",replace e,n,delete t and keep "ial".

So,the cost is 4+2+2=8.

(Thinking)

 

[I like Serena]

Why should it be T(6,6)=5? (Thinking)
Don't we have two replace all the 6 letters e,x,p,o,n,e by these ones: p,o,l,y,n,o ?
If we would keep "po" and "n",wouldn't it be like that:

delete e,x -> cost=4
keep po-> cost=0
insert l,y-> cost=4
keep n-> cost=0
replace e by o-> cost=1

So,wouldn't the cost be $9$ ?

Or have I done somrthing wrong?

But if we replace all 6 letters, except 'n' because it's the same, wouldn't we have a cost of 5? (Wondering)

Oh yes,you are right! (Nod)

So..to calculate T(11,10) , do we have to do the following?

replace all the letters from e till o,keep "n",replace e,n,delete t and keep "ial".

So,the cost is 4+2+2=8.

(Thinking)

I think so! (Nod)

 

[evinda]

But if we replace all 6 letters, except 'n' because it's the same, wouldn't we have a cost of 5? (Wondering)

Oh yes..you are right! (Wasntme)

So,everything is wrong from T(6,6) till the end of the row,right? (Thinking)

I think so! (Nod)

Great! (Cool)

 

[I like Serena]

Oh yes..you are right! (Wasntme)

So,everything is wrong from T(6,6) till the end of the row,right? (Thinking)

And also on the rows that come after I'm afraid. (Doh)