Counterfactual Expectation Calculation

[Ackbach]

$\newcommand{\doop}{\operatorname{do}}$
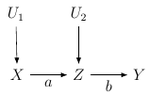
Problem: (This is from Study question 4.3.1 from Causal Inference in Statistics: A Primer, by Pearl, Glymour, and Jewell.) Consider the causal model in the following figure and assume that $U_1$ and $U_2$ are two independent Gaussian variables, each with zero mean and unit variance.

Find the expected salary of workers at skill level $Z=z$ had they received $x$ years of college education. [Hint: Use Theorem 4.3.2, with $e:Z=z,$ and the fact that for any two Gaussian variables, say $X$ and $Z,$ we have $E[X|Z=z]=E[Z]+R_{XZ}(z-E[Z]).$ Use the material in Sections 3.8.2 and 3.8.3 to express all regression coefficients in terms of structural parameters, and show that $$E[Y_x|Z=z]=abx+\frac{bz}{1+a^2}.]$$

View attachment 9643

Here, $X$ is education, $Z$ is skill, and $Y$ is salary. The accompanying SEM is
\begin{align*}
X&=U_1\\
Z&=aX+U_2\\
Y&=bZ.
\end{align*}

My Work So Far:
We are called on to compute $E[Y_x|Z=z].$
Now Theorem 4.3.2 states: Let $\tau$ be the slope of the total effect of $X$ on $Y,$
$$\tau=E[Y|\doop(x+1)]-E[Y|\doop(x)] $$
then, for any evidence $Z=e,$ we have
$$E[Y_{X=x}|Z=e]=E[Y|Z=e]+\tau(x-E[X|Z=e]).$$
For our problem, with $e:Z=z,$ we have
$$E[Y_{X=x}|Z=z]=E[Y|Z=z]+\tau(x-E[X|Z=z]).$$
Not sure where to go from there.

Now I know that this is a non-deterministic counterfactual problem, which means the process should be:

1. Abduction: Update $P(U)$ by the evidence to obtain $P(U|E=e).$
2. Action: Modify the model, $M,$ by removing the structural equations for the variables in $X$ and replacing them with the appropriate functions $X=x,$ to obtain the modified model, $M_x.$
3. Prediction: Use the modified model, $M_x,$ and the updated probabilities over the $U$ variables, $P(U|E=e),$ to compute the expectation of $Y,$ the consequence of the counterfactual.

So, for abduction, am I right in thinking that the only evidence we're using right now is $Z?$ In that case, we want to determine the $U_1$ and $U_2$ that correspond to $Z=z.$ We have the two equations
\begin{align*}
X&=U_1\\
z&=aX+U_2,
\end{align*}
or
\begin{align*}
X&=U_1\\
z-aX&=U_2.
\end{align*}
Without knowing the pre-condition value of $X,$ it's not clear how to continue. How do I continue? I'm also really not understanding the hint. Any thoughts about the hint?

Thanks for your time!

Note: I have cross-posted this at Cross-Validated:

https://stats.stackexchange.com/questions/457740/counterfactual-expectation-calculation

 

[Ackbach]

I have obtained access to the full solutions manual, after contacting Wiley about it. I will not type up the solution in full, but simply note a few critical pieces of information I was missing in order to answer this question:

1. $E[x|z]=\beta_{xz}\,z,$ because of the model, and the relationship between $x$ and $z.$ Here $\beta_{xz}$ is the regression coefficient, as in $X=\beta_{xz}Z.$
2. Reversing regression coefficients requires knowing the variances: $\beta_{xz}\sigma_z^2=\beta_{zx}\sigma_x^2.$
3. The slope of the total effect, $\tau,$ you can read off the diagram as $\tau=ab.$
4. Variances add like this: if $Z=aX+U_2,$ then $\sigma_z^2=a^2\sigma_x^2+\sigma_{U_2}^2.$

This is sufficient information to obtain the desired result.