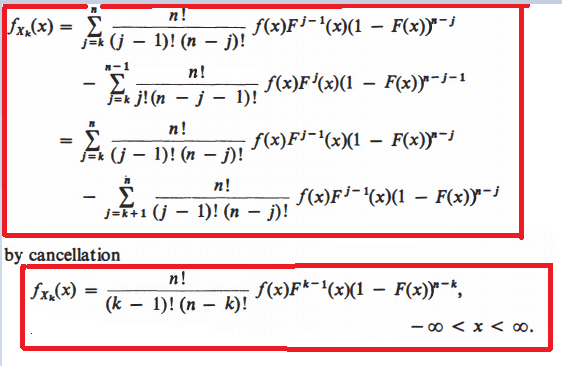SUMMARY
The discussion centers on the derivation of the probability density function (PDF) from the distribution function for a random variable. The author successfully computed the PDF, denoted as ##f_{X_k}(x)##, using the cumulative distribution function (CDF) ##F_{X_k}(x)##, expressed as ##F_{X_k}(x) = p(X \leq x) = \displaystyle\sum_{j=k}^n \binom{n}{j} F^j(x)(1-F(x))^{n-j}##. The final result is confirmed as ##f_{X_k}(x) = \frac{n!}{(k-1)!(n-k)!}f(x) F^{k-1}(x)(1-F(x))^{n-k}##, demonstrating a clear understanding of the computations involved.
PREREQUISITES
- Understanding of cumulative distribution functions (CDF)
- Familiarity with probability density functions (PDF)
- Knowledge of binomial coefficients and their properties
- Basic calculus, particularly differentiation and integration of functions
NEXT STEPS
- Study the properties of cumulative distribution functions (CDF) in detail
- Learn about the relationship between probability density functions (PDF) and cumulative distribution functions (CDF)
- Explore binomial distributions and their applications in probability theory
- Investigate advanced topics in statistical inference, including maximum likelihood estimation
USEFUL FOR
Statisticians, data scientists, and students of probability theory who are looking to deepen their understanding of the relationship between cumulative distribution functions and probability density functions.