Desymmetrization of a combinatorial set

[lavoisier]

Hello, here's a problem at the boundary between mathematics, programming and chemistry, which I'm struggling with, but I guess can be easily solved by mathematicians/programmers.
I'll explain it as concisely as I can, but sorry, it will be a long post, it's not that trivial.

In chemistry there is an operation called 'R group decomposition' that is performed on a set of molecules to analyse the structural determinants of some of their properties.
Here's an example of template ('scaffold') that can be used:

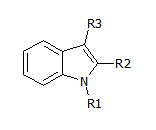
There is some software that takes this template + a set of molecules, checks which ones 'match' the template and lists the corresponding R1, R2 and R3. These are the 'R groups', and taken together with the scaffold, uniquely identify a molecule. So far so good.
However, there are templates that, by effect of symmetry and chemical rules, can produce several valid sets of R groups. For instance this one:

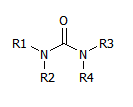
Symmetry shows that R1,R2 can be swapped with R3,R4.
Chemistry shows that R1 and R2 can be swapped, and so can R3 and R4.
So, a molecule like this one:

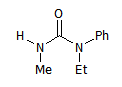M1
has 8 'mappings':
M1_{R1,R2,R3,R4}={H,Me,Ph,Et},{H,Me,Et,Ph},{Me,H,Ph,Et},{Me,H,Et,Ph},{Ph,Et,H,Me},{Ph,Et,Me,H},{Et,Ph,H,Me},{Et,Ph,Me,H}.
Each of these mappings is perfectly valid. If one were only interested in identifying molecules, choosing anyone mapping at random would be OK.

The problem is that, when analysing the properties of a set of molecules, it is desirable to minimise the number of distinct 'descriptors' at each R-position and maximise the sum of all pairwise differences of numbers of descriptors; choosing mappings at random does not achieve that.

Example: suppose that we choose the first mapping for M1:
M1_{R1,R2,R3,R4}={H,Me,Ph,Et}
In terms of descriptors at each R position, we have: {R1}={H}, {R2}={Me}, {R3}={Ph}, {R4}={Et}.

Now we add this molecule to the set:

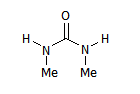M2
Due to the identity between some groups, the non-degenerate mappings are fewer:
M2_{R1,R2,R3,R4}={H,Me,H,Me},{H,Me,Me,H},{Me,H,Me,H},{Me,H,H,Me}.

It is inevitable to add new descriptors to 'some' R positions.
If we choose the first mapping of M2, we're doing well, because we don't add any new descriptor to R1 or R2, and we're adding new descriptors only to R3 and R4.
M2_{R1,R2,R3,R4}={H,Me,H,Me}
And we have now: {R1}={H}, {R2}={Me}, {R3}={Ph,H}, {R4}={Et,Me}.
The number of descriptors in each R position is just the number of distinct elements in each of these sets (so 1, 1, 2, 2 here). The total number of descriptors is the sum of the above, so here 1+1+2+2=6 (you don't consider equal the H in R1 and the H in R3, because at this point they are desymmetrised.
Obviously if we had chosen the 3rd mapping for M2, we would have added one new descriptor to each position, ignoring the fact that H was already in R1 and Me in R2.

It may seem simple: just choose for each new molecule the mapping that adds the fewest descriptors.
But it's not. First, you don't really add the molecules one by one: you already have a large set of molecules (e.g. 500) with all their combinatorial mappings (could be from 2 to 8, typically, for each molecule), and in the end you need to choose one mapping per molecule in such a way that the above conditions are satisfied (minimal sum of different descriptors, maximal sum of differences of numbers of descriptors). I don't need to tell you how many possible combinations that would make, if one wanted to approach this by brute force :O)

So I went for what I thought was a more 'clever' approach.
I tried this: pick one arbitrary mapping for the first molecule and then run iterations among the rest of the set to choose at each cycle one mapping that gives the lowest addition of descriptors overall, and within this condition, adds the new descriptors preferably to groups that already have more descriptors.
Computationally, I just made a vector like {1,0,0,1} for each mapping, comparing existing descriptors with the one in the mapping, 1 for not present, 0 for already present. Then I made a SUM composed by the norm of the vector (in this case 2) multiplied by 10⁴, + the individual vector components each multiplied by 10ⁱ, where i is the appropriately chosen exponent from 0 to 3, based on the sorting by descriptor counts in the current reference sets of descriptors in the R positions. So you have 10001 for a mapping that adds 1 new descriptor to the R position that already has the most descriptors. 10010 would indicate adding 1 new descriptor to the R position that has the second most descriptors, and so on, 20011 would add 1 to each the most populated R position and the second most populated one. So at each cycle only mappings with the lowest SUM are considered, and only one of them is selected (because two mappings with SUM 10001 don't necessarily add the same descriptor to that position). The corresponding molecule passes, the reference R position sets of descriptors are updated, all other molecules are sent to the next iteration.

This seemed to work to some extent, but by running some tests I found that the initial choice, and even the order of the molecules, resulted in different end sets, some with a good separation of descriptors, some less good, and even the total number of descriptors varied a bit.
Example: in one run I got something like 13, 80, 220, 262; in another run something like 40,65,250,230.

This is not good. The solution should not only be unique, but also optimal. I'm not sure it can be independent from the initial choice of mapping for the first compound, but then there should be a way to choose that best.

Here's an example set:
M1 ={H,Me,Ph,Et},{H,Me,Et,Ph},{Me,H,Ph,Et},{Me,H,Et,Ph},{Ph,Et,H,Me},{Ph,Et,Me,H},{Et,Ph,H,Me},{Et,Ph,Me,H}
M2 ={H,Me,H,Me},{H,Me,Me,H},{Me,H,Me,H},{Me,H,H,Me}
M3={H,H,Me,Me},{Me,Me,H,H}

Can anyone please suggest an approach to tackle this?
Am I missing something obvious?
I have a vague idea that sorting may help, e.g. sort all mappings by the overall frequency of each descriptor by R position, but if my selection procedure is not good...

Any help would be appreciated.

Thanks!
L

 

[lavoisier]

Just adding some info, as I studied the problem a bit more today.

To be less vague concerning the objective:
- we want to have the minimal possible total number of [distinct descriptor x position] combinations (this is the most important condition); so if 1,3,6,8 --> 18 can be obtained, 1,2,8,12 --> 23 is not an acceptable solution.
- the distribution of distinct descriptors among the different positions should be as asymmetrical as possible, meaning that the first position should have as few distinct descriptors as possible; then the second as few as possible within the set that respects the previous condition, and so on.

The approach I tried today was to calculate first the frequency of each descriptor in its own R position column. So in the case above you would have:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 5 5 2 2
Me H Et Ph 5 5 2 2
H Me Ph Et 5 5 2 2
Me H Ph Et 5 5 2 2
Et Ph H Me 2 2 5 5
Ph Et H Me 2 2 5 5
Et Ph Me H 2 2 5 5
Ph Et Me H 2 2 5 5
H Me H Me 5 5 5 5
Me H H Me 5 5 5 5
H Me Me H 5 5 5 5
Me H Me H 5 5 5 5
H H Me Me 5 5 5 5
Me Me H H 5 5 5 5

where each molecule is a different colour.
If I wanted to have the smallest set of descriptors in R1, I could choose only rows that contain H (a descriptor with the highest frequency in R1), because there is at least one H in R1 in each molecule.
So the above table would become:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 5 4 1 1
H Me Ph Et 5 4 1 1
H Me H Me 5 4 1 2
H Me Me H 5 4 2 1
H H Me Me 5 1 2 2

That's already an improvement: from 14 rows to 5.
I could have chosen Me instead of H, as it had the same frequency.

Now, looking at R2, I see that the smallest set must include both Me and H. If I excluded H, I would leave out the green molecule.
There is no reduction of rows at this stage.

For R3, the smallest set is Et + Me, reducing the table to:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 3 2 1 1
H Me Me H 3 2 2 1
H H Me Me 3 1 2 1

which is a solution with 1,2,2,3 --> 8 total position x descriptor cases.

I don't know how to apply this computationally, if it gives the best solution, or a single solution for that matter, and how to choose in cases like R3 above where Et+Me or Ph+Me seem equivalent.
But this all looks much like set operations to me...

 

[Stephen Tashi]

it is desirable to minimise the number of distinct 'descriptors' at each R-position

You example made clear what that requirement means.

and maximise the sum of all pairwise differences of numbers of descriptors

I don't understand what numerical computation that refers to.

 

[mfb]

Looks like a graph theory problem. And if I am right, even the easiest case is very hard.

Let's formalize it a bit: For a given scaffold, you can split the attached functional groups into sets that attach to different places. As an example, R1, R2 and R3 are separate sets in the first example. You can look at each set separately, as anything that happens within other sets is irrelevant.

If such a set just has a single functional group, there is nothing to do. Other cases:

- a set can consist of two functional groups.
- a set can consist of three functional groups. Here I see two subcases, can you confirm those?
-- three groups with fixed parity: R1 R2 R3, R2 R3 R1, R3 R1 R2 are the same, but those are different from R1 R3 R2, R3 R2 R1, R2 R1 R3. An example would be three groups attached to a single carbon atom.
-- three groups with open parity: All 6 options from above are equivalent. I guess this can happen when part of a ring for example.
- a set can consist of four functional groups. Here partity gets worse:
-- We can have 4 groups in a tetrahedron, with parity similar to the three-group case
-- We can have 4 groups in a ring, which leads to three subgroups (e.g. by picking the group opposite of R1)
-- I don't know if the 4 groups can all be completely equivalent
- 5 or more functional groups. Parity considerations get worse the more groups we get.

- In addition to those elementary sets, two or more sets can form a larger set. This happens in the second example in post 1. This can repeat for more layers, making a complex hierarchy.

Notation:
For functional groups, I'll use capital letters: A, B, C, ...
For a given substance, I'll put the functional groups into sets as described above. The second example could get a molecule like {{A,B},{C,D}} where {A,B} is bound to one nitrogen atom and {C,D} is bound to the other one. I'll ignore the parity issues for now.
For a given representation of a substance, I'll use square brackets: [[A,B],[C,D]] is putting A at R1, B at R2 and so on.

The goal is now to assign a representation for every substance, such that the sum of (distinct letters in each position) is minimized. If there is more than one solution with the same sum, we get the additional constraint that the individual numbers should be as different as possible, where Stephen Tashi asked for clarification how exactly that has to be evaluated.

Something I can rule out: Going by frequency does not always work. You can always change the frequencies arbitrarily by adding molecules that don't change the optimal assignment of the existing molecules.

Let's start with the easiest case first: Two functional groups that can be exchanged. We can represent the functional groups by vertices in a graph, and molecules are edges connecting two vertices.
If a vertex appears in one place (R1 or R2) only, color it green or red, respectively, otherwise don't color it. No edge is allowed to connect two vertices with the same color. The problem now asks for the largest number of vertices we can color while keeping the edge condition.

If the graph is not connected, we can optimize all individual parts separately, restrict the analysis to connected parts.
While we can have multiple edges connecting the same vertices (if the molecules differ in other functional groups), those don't change anything. We can reduce it to a single edge.
Every vertex A that has an edge AA (a loop, a molecule having the same functional group in both places) cannot be colored. This also means we can remove all edges involving A from the analysis: They won't violate the edge condition anyway.
Every vertex A that has a single edge AB can be ignored for the optimization: If B has a color, assign the opposite color to A, otherwise assign a random color to it.
Our optimization problem is now reduced to a connected, simple graph where every vertex has at least two edges.
Every cycle of odd length needs at least one uncolored node. This is the only condition. The question is now "how can we select a minimal number of vertices such that the remaining graph (without those vertices) has no cycle of odd length?" A graph without odd-length cycles is called bipartite, so we look for a maximal bipartite subgraph. If we would remove edges instead of vertices, it has been shown that this problem is NP-complete: For large graphs, there is no efficient algorithm that will always find the best case in a reasonable time. I didn't find a discussion of this, but I would expect that to be true if we remove vertices instead of edges as well.If the last assumption is true, then even the easiest possible case - just two functional groups in the molecule - does not have a reasonable ideal solution for very large numbers of molecules. Can you live with good approximations? Those can be much easier to find.

 

[lavoisier]

Thank you @mfb for your detailed analysis. It is quite above my level, to be honest.

First I will add some info from the work I did today on the problem.
I spotted a conceptual error in my frequency approach above.
In fact what I needed to compute was the number of molecules in which each descriptor was present, not how many times in total it was present. And I needed to sort the set by this new frequency first and then by the descriptor itself.
This way, starting from R1, if one picks the rows, for each molecule, where the frequency is the same as the one of the top row and the descriptor is also the same as the top row, one always minimises the number of distinct descriptors in R1.

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 3 3 1 1
Me H Et Ph 3 3 1 1
H Me Ph Et 3 3 1 1
Me H Ph Et 3 3 1 1
Et Ph H Me 1 1 3 3
Ph Et H Me 1 1 3 3
Et Ph Me H 1 1 3 3
Ph Et Me H 1 1 3 3
H Me H Me 3 3 3 3
Me H H Me 3 3 3 3
H Me Me H 3 3 3 3
Me H Me H 3 3 3 3
H H Me Me 3 3 3 3
Me Me H H 3 3 3 3

It doesn't make a difference in this specific case, but there are cases where equal frequencies apply to different descriptors.
The other thing that I changed was this: at each step I calculated the number of distinct descriptors that one would obtain in each position by the above mechanism (including sorting each time of course).
In the example, R1 would have 1 (H), and so would all other R's, because this is the combinatorial set where everything is symmetrical.
I had a doubt whether, after processing R1, the set would be desymmetrised, i.e. whether it would make a difference to process next R2 rather than R3 or R4.
To my surprise, I found that it did make a difference. See for instance:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 3 2 1 1
H Me Ph Et 3 2 1 1
H Me H Me 3 2 1 2
H Me Me H 3 2 2 1
H H Me Me 3 1 2 2

Min distinct for each choice: R1=1, R2=2, R3=2, R4=2. So in this case there is no difference.
But I had other more complicated cases where the process went like R1 -> R3 -> R4 -> R2, and it gave a different result compared to processing the R positions in the order I decided arbitrarily.
Trouble is that if I process R2 next, I assign it Me and H. If I process R3, I assign Et and Me. If I process R4, I assign Et and Me as well.
In the case of R3, that would leave me with:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Et Ph 3 2 1 1
H Me Me H 3 2 2 1
H H Me Me 3 1 2 2

1,2,2,3

In the case of R4:

R1 R2 R3 R4 f(R1) f(R2) f(R3) f(R4)
H Me Ph Et 3 2 1 1
H Me H Me 3 2 1 2
H H Me Me 3 1 2 2

1,2,3,2

This seems to imply that the choice of what position to work on one makes at each step is relevant to what happens afterwards, but I don't know how one should choose.
Maybe I should choose the R position that not only spans the minimal number of distinct descriptors, but also has the highest 'average' frequency?
Just guessing though.

Another element I can add to this discussion is that there is some proprietary software that does this kind of job on large sets (>500) of molecules in a matter of seconds, so I suppose they are using an approximation.
By some tests I found that, for instance, my procedure above gave R1,R2=7,195 --> 202 descriptors; the proprietary software gave 20,180 --> 200.
In another case with 4 R positions, something like R1,R2,R3,R4 = 6,13,53,305 --> 377; the software 13,80,202,58 --> 353.
So I suppose my procedure is better at making the minimal possible set of descriptors by each position, but not overall.

Maybe I could first run a linear programming routine to reduce the initial set to a set that gives the minimal number of descriptors overall, and then process this as above?

So to answer your question @mfb , yes, I would really like any method that gives me an approximated solution.
But I have no idea how to translate the graph theory you explained into code. I'd need an example.

Again, many thanks for your input!
Have a good weekend
L

 

[jim mcnamara]

Hmm. I wonder if @TeethWhitener has seen this thread. It kind of straddles some areas he is seems to be familiar with I believe. It is worth a try anyway.

 

[TeethWhitener]

Thanks for thinking of me, but I'm not sure I can be of much help. Like Stephen Tashi, I'm stumped on what exactly the "maximize sum of differences" condition means. It's also unclear to me what the end goal is. For your urea example, you can interchange {R1,R2} with {R3,R4} by symmetry and R1 (or R3) with R2 (or R4) by a rotation about the C-N bond (forming a group), so I'm wondering if storing a set of equivalence transformations along with each individual scaffold might be a different way to treat the problem, to eliminate the preponderance of equivalent mappings for sets of individual molecules with the same scaffold. But again, I'm not sure if that helps with your problem, mainly because I'm not sure what your problem is exactly.

 

[lavoisier]

Hello all, thanks for you input.
You're right, my formulation of the conditions was not clear. I'll reformulate them in a simpler way.

When molecules have certain symmetries, the software component that does the 'R groups decomposition' returns for each molecule all possible 'mappings', like in my example for 3 molecules (1 molecule = 1 colour):

R1 R2 R3 R4
H Me Et Ph
Me H Et Ph
H Me Ph Et
Me H Ph Et
Et Ph H Me
Ph Et H Me
Et Ph Me H
Ph Et Me H
H Me H Me
Me H H Me
H Me Me H
Me H Me H
H H Me Me
Me Me H H

The aim is simply (!) to choose one and only one mapping per molecule in such a way that:
1 - the sum of the numbers of distinct descriptors at each R-position is minimal
2 - within the boundaries set by condition 1, the descriptors are spread between R-positions so that each position, in sequence, has the minimal possible number of descriptors

So in the example, this choice:

R1 R2 R3 R4
H Me Et Ph
Me H H Me
Me Me H H

would be bad, because it puts 2 distinct descriptors in R1 (H and Me), 2 in R2 (H and Me), 2 in R3 (Et and H) and 3 in R4 (H, Me and Ph), for a total of 9.
A solution satisfying condition 1 would instead be:

R1 R2 R3 R4
H Me Et Ph
H Me H Me
H H Me Me

which has: (R1)=1, (R2)=2, (R3)=3, (R4)=2, for a total of 8.

This one would also be valid:

R1 R2 R3 R4
H Me Et Ph
H Me H Me
Me Me H H

which has: (R1)=2, (R2)=1, (R3)=2, (R4)=3, for a total of 8.
(I don't think we can go below 8).
The order in which the numbers of distinct descriptors come doesn't matter, as long as their total is minimal.

As for condition 2, I don't think I can show it in this example, because all solutions with a total of 8 seem to meet it.
But I can tell you, after running tests on larger sets, that situations like this occur:

(R1),(R2) = 20,180 --> 200
(R1),(R2) = 10,190 --> 200
(R1),(R2) = 6,194 --> 200

where the third solution is the preferred one, as it puts the minimal possible number of descriptors in R1.
In cases with 4 descriptors, you may have to choose between:

(R1),(R2),(R3),(R4) = 60,30,10,100 --> 200
(R1),(R2),(R3),(R4) = 5,61,101,33 --> 200
(R1),(R2),(R3),(R4) = 5,70,23,102 --> 200

where again the 3rd solution is the preferred one, because if you sort the numbers in ascending orders:

10,30,60,100
5,33,61,101
5,23,70,102

solution 3 puts the minimal numbers of descriptors 'as early' as possible.
E.g. if we turned the numbers into ranks:

3,2,1,1 --> 3211
1,2,2,2 --> 1222
1,1,3,3 --> 1133

1133 being the smallest number, the third solution is chosen.

The algorithm based on frequencies does a decent job at meeting condition 2, but then condition 1 may not be met.
The one based on choosing at each iteration the mapping that adds the fewest substituents is slow and depends on the initial order of molecules.
Maybe if I combined the two...

The other possibility is to write this as a linear programming problem with binary solution vector.
So from the initial table:

R1 R2 R3 R4 M1 M2 M3
H Me Et Ph 1 0 0
Me H Et Ph 1 0 0
H Me Ph Et 1 0 0
Me H Ph Et 1 0 0
Et Ph H Me 1 0 0
Ph Et H Me 1 0 0
Et Ph Me H 1 0 0
Ph Et Me H 1 0 0
H Me H Me 0 1 0
Me H H Me 0 1 0
H Me Me H 0 1 0
Me H Me H 0 1 0
H H Me Me 0 0 1
Me Me H H 0 0 1
condition =1 =1 =1

this says that a single mapping must be chosen for each molecule M.

Then we need to count the number of distinct descriptors at each position, sum them and minimise the sum.

This is not obvious to do, but @andrewkirk once gave me a very useful tip for a similar problem, which I can adapt to this case.
It is a bit complicated, I won't write it down, but in essence you compute the overall set of descriptors (here H, Me, Et, Ph), make the cartesian product of that by the R positions, and add a model matrix column for each resulting descriptor and position, e.g. R1=H, R2=H, R3=H, R4=H, R1=Me ... R4=Ph.
Then you add appropriate rows with the negated sum (-N) of each Ri=Dj frequency, and impose that to be <=0 and >-N, and the corresponding coefficient column entries set to 1. The product of the solution vector by the coefficient column will then give the overall number of distinct descriptors.

I think this approach will definitely work for condition 1. But I don't think I can adapt it for condition 2.
And the other problem is that, even for this simple example, I would have 3 + 4*4*2 = 35 constraint columns and a solution of 8+4+2+4*4 = 30 unknowns.
My typical problem may have 350 molecules with up to 2800 mappings, 77 overall descriptors over 4 positions --> 350 + 77*4*2 = 966 constraints, 2800 + 77*4 = 3108 unknowns.
Now, R's lpSolve is very good, but I don't know if it can handle that in a reasonable time.

And there is always the nagging fact that some commercial software can do this in seconds...

 

[lavoisier]

Here's a link related to this problem:

https://www.schrodinger.com/sites/default/files/s3/mkt/Documentation/2016-4/docs/rgroup_user_manual/rgroup_analyze_core.htm

In particular the last sentence:

When using these two methods, the program must decide which mapping to use for each input structure if the core substructure maps to some input structures in several ways. The program picks the best set of mappings chiefly by optimizing the fingerprint similarity of the side chains for pairwise alignments of the input structures. This choice usually also minimizes the number of R-group positions defined on the core.

I think they're saying they try to keep 'similar' descriptors in the same positions.
In our example, H is more similar to Me than to Ph.
Mmh... not sure it will work optimally in all cases. And there's this 'usually'...