Sure thing!

The Law of Sines is a ratio. The neat thing about this law is that it works for ANY triangle. It's a secret that those geometry teachers forbid to tell their students :D
The formula for the law of sines is $$ \frac{a}{sin(A)} = \frac{b}{sin(B)} = \frac{c}{sin(C)}$$
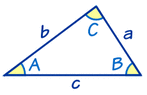
The angles are represented by the upper case letters, while the lower case letters are the side of the triangle, as seen in the image below.
https://www.physicsforums.com/attachments/2826
So in your second image, you have two angles, the first being 90 degrees, and the second 67. Since a triangle is known to have 180 total degrees, we subtract 90 and 67 to get our third angle:
$$180-90 = 90$$
$$90-67 = 23$$
So all three angle values are known now, which are 90, 67, and 23 degrees. :)
We have one known value of length, which is all we need. That is the value of 10 ft, which is OPPOSITE of our angle that measures 23 degrees. This means that we have enough information to solve for the remaining sides. So now we set up the ratio. I figure there is more than one way to do it, but this is how I do it. We have both a values (Both uppercase and lowercase a. I'm calling the distance of 10 feet lowercase a and the value of 23 degrees uppercase A because they are opposite of each other in your diagram and as shown in the image above). So, let's see what we have:
$$\frac{10}{sin(23)} = \frac{c}{sin(90)}$$
The angle C is 90 degrees because it is opposite of the value c that you are trying to find in the diagram. :)
So now, we just treat this as a typical ratio and solve for c:
$$\frac{10}{sin(23)} = \frac{c}{sin(90)}$$
A pretty handy thing to know in trigonometry and even geometry is that the sine of 90 degrees = 1. So now, we'll rewrite:
$$\frac{10}{sin(23)} = \frac{c}{1}$$
Now we cross multiply:
$$\frac{10}{sin(23)} = \frac{c}{1}$$
I'm going to multiply 1 by 10 (Diagonal to each other), then divide by $$sin(23)$$ . This will give us our answer:
$$1*10 = 10$$
$$\frac{10}{sin(23)} = c$$
Approximately equals 25.59304665
If you have any questions, or would like to see the other side done as well, I'd be happy to!