Determine the confidence interval

[mathmari]

Hey!

(a) In winter, the roads around Lake Macatawa are salted. To study the impact of this on Lake Macatawa, students took $32$ water samples from the western basin of the lake and Sodium content (in parts per million, ppm) determined. As a result, the students have receive the following data:

(i) Calculate the sample mean.
(ii) Calculate the adjusted sample variance.
(iii) Assume a normal distribution and determine a two-sided confidence interval for the above sample for the mean sodium content with a confidence level of $0.95$. Also enter the used quantile and its (approximate) value.(b) In addition, $35$ water samples were collected from the eastern basin of Lake Macatawa and in each case the sodium content (in ppm) was measured. This resulted in a sample mean of $24.11$ and an adjusted sample variance of $24.44$. Assume a normal distribution.
(i) Determine a two-sided confidence interval for the mean sodium content with a confidence level of $0.9$. Also enter the quantile used and its (approximate) value.
(ii) Determine a confidence interval of the form $(-\infty, h]$ for the mean sodium content with a confidence level of $0.9$. Also state the one used quantile and its (approximate) value.(c) The PCB content was determined from a sample of fish from Lake Michigan (in ppm). It is known that the standard deviation is $0.8$ ppm. Assume a normal distribution. The below were measured:

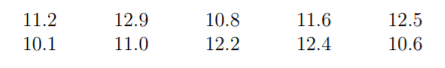
(i) Calculate the sample mean and determine a two-sided confidence interval for the above sample for the mean PCB content with a confidence level of $0.99$. Also enter the used quantile and its
(approximate) value.
(ii) Determine a confidence interval of the form $(-\infty, h]$ for the above sample for the mean PCB content with a confidence level of $0.99$. Give also the quantile used and its (approximate) value.
I have done the following :

(a) (i) We add all elements and divide the result by the number of elements. So the sample mean is equal to \begin{align*}\overline{x}_{32}=& \frac{1}{32}\left(13.0 +18.5 +16.4 +14.8 +19.4+ 17.3 +23.2 +24.9 +20.8 +19.3 +18.8 +23.1 +15.2+ 19.9 +19.1+ 18.1 +25.1+ 16.8+ 20.4 +17.4 +25.2+ 23.1 +15.3+ 19.4 +16.0 +21.7 +15.2+ 21.3+ 21.5 +16.8+ 15.6 +17.6 \right )\\ & =\frac{1}{32}\cdot 610.2=19.06875\end{align*} Is that correct ? :unsure:

(ii) We have that \begin{align*}s_{32}^2&=\frac{1}{32-1}\sum_{i=1}^{32}(x_i-\overline{x}_{32})^2=\frac{1}{31}((13.0-19.06875)^2 +(18.5-19.06875)^2 +(16.4-19.06875)^2 \\ &+(14.8-19.06875)^2 +(19.4-19.06875)^2+ (17.3-19.06875)^2 +(23.2-19.06875)^2 \\ &+(24.9-19.06875)^2 +(20.8-19.06875)^2 +(19.3-19.06875)^2 +(18.8-19.06875)^2 \\ &+(23.1-19.06875)^2 +(15.2-19.06875)^2+ (19.9-19.06875)^2 +(19.1-19.06875)^2\\ &+ (18.1-19.06875)^2 +(25.1-19.06875)^2+ (16.8-19.06875)^2+ (20.4-19.06875)^2 \\ &+(17.4-19.06875)^2 +(25.2-19.06875)^2+ (23.1-19.06875)^2 +(15.3-19.06875)^2\\ &+ (19.4-19.06875)^2 +(16.0-19.06875)^2 +(21.7-19.06875)^2 +(15.2-19.06875)^2\\ &+ (21.3-19.06875)^2+ (21.5-19.06875)^2 +(16.8-19.06875)^2+ (15.6-19.06875)^2 \\ &+(17.6-19.06875)^2 )\\ & = \frac{1}{31}\cdot 328.54875\\ & \approx 10.59835\end{align*} Is that correct ? :unsure:

(iii) Do we use the formula \begin{equation*}\left [M(x)-\frac{\sigma}{\sqrt{n}}q_{1-\frac{a}{2}},M(x)+\frac{\sigma}{\sqrt{n}}q_{1-\frac{a}{2}}\right ] \end{equation*} where $M(x)$is the mean, i.e. $M(x)=19.06875$ ? Is $\sigma$ equal to the square root of the result of (b) ? The value of $q$ is related to the confidence level, right? :unsure:

 

[I like Serena]

Hey mathmari!

a.i and a.ii look correct to me. (Nod)
In a.iii we do not have $\sigma$, which is unknown. Instead we have $s$, which is the standard deviation of the sample. It is indeed the square root of the result of a.ii.

The value of $q$ is indeed related to the confidence interval. Can we find it?

 

[mathmari]

In a.iii we do not have $\sigma$, which is unknown. Instead we have $s$, which is the standard deviation of the sample. It is indeed the square root of the result of a.ii.

The value of $q$ is indeed related to the confidence interval. Can we find it?

Ahh ok!

So we use the formula $$\left [M(x)-\frac{\sqrt{V^{\star}}}{\sqrt{n}}t_{n-1,1-a/2}, \ M(x)+\frac{\sqrt{V^{\star}}}{\sqrt{n}}t_{n-1,1-a/2}\right ]$$ right?
Do we have $V^{\star}=s_{32}^2=10.59835$, $M(x)= 19.06875 $ and $t_{n-1,1-a/2}=t_{31,0.975}= 2,037$ ? :unsure:

So we get \begin{equation*}\left [19.06875-\frac{\sqrt{10.59835}}{\sqrt{32}}\cdot 2.037, \ 19.06875+\frac{\sqrt{10.59835}}{\sqrt{32}}\cdot 2.037\right ]\approx \left [17.89646, \ 20.24104\right ]\end{equation*} right? :unsure:

 

[I like Serena]

Ahh ok!

So we use the formula $$\left [M(x)-\frac{\sqrt{V^{\star}}}{\sqrt{n}}t_{n-1,1-a/2}, \ M(x)+\frac{\sqrt{V^{\star}}}{\sqrt{n}}t_{n-1,1-a/2}\right ]$$ right?
Do we have $V^{\star}=s_{32}^2=10.59835$, $M(x)= 19.06875 $ and $t_{n-1,1-a/2}=t_{31,0.975}= 2,037$ ?

So we get \begin{equation*}\left [19.06875-\frac{\sqrt{10.59835}}{\sqrt{32}}\cdot 2.037, \ 19.06875+\frac{\sqrt{10.59835}}{\sqrt{32}}\cdot 2.037\right ]\approx \left [17.89646, \ 20.24104\right ]\end{equation*} right?

Looks right to me. (Nod)