Determining optimum flywheel dimensions

[motoxYogi]

Hello all,

I am currently doing a design project on gyroscopes.
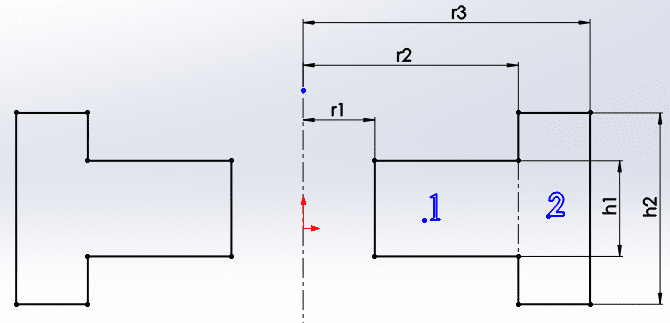
My question concerns the flywheel design, specifically trying to determine the dimensions of a flanged free-spinning flywheel to maximize the moment of inertia while trying to minimize the mass, given certain design constraints.
I've treated the flanged flywheel as two separate hollow cylinders and as far as I understand it, the moment of inertia about the axis of rotation is
I=1/2[m₁(r₁²+r₂²)+m₂(r₂²+r₃²)]
The mass is
M=πρ[h₁(r₂²-r₁²)+h₂(r₃²-r₂²)]
Due to design constraints r₃=0.05m and h₂ has a maximum size of 0.04m, due to the bearing I will be using r₁ = 0.011 m and h₁=0.007m. So the only variable is r₂.
The material that i have been using is brass, ρ=8400kg/m³

I know I should be able to use calculus to solve it but I've never been able to apply it well, I've been chasing myself round in circles for days and just keep drawing blanks.
Any help or suggestions is greatly appreciated.

 

[motoxYogi]

I've been using Excel to perform iterative calculations and then plotted the MOI and mass against r2.
resulting in this graph

I then tried to approximate where the slope of MOI dropped off significantly compared to the the slope of the mass.
Would this be an acceptable approximation?

 

[xxChrisxx]

Plot MOI/Mass vs R2.

Also you can use a subtraction to delete mass (ie lightning it) from the MOI and mass calcs. Assume that all the force acts on the radius of the COM of the deleted segment.

 

[motoxYogi]

Hmmm...
I tried the MOI/mass vs. r2. The maximum point on the curve corresponded to r2 = 42.5 mm.
I then got the bearing resistances for that mass and MOI and plugged it into another excel spreadsheet to determine the maximum spin time it would achieve given initial velocity 1047 rad/sec.
It worked out at approximately 460 seconds. The values I approximated (r2 = 28 mm) worked out at about 550 seconds. When I initially wrote the equations for spin time I was trying to select a bearing, I used a best guess for r2 = 30 mm and it gives me a spin time of 700 sec!
Maybe I should have mentioned the fact that I'm using hybrid bearings, I was just reading through the manufacturers brochure again and realized that it called for a minimum radial load of 16.4 N (1.67kg) for my purposes.
The mass at r2 = 42.5 mm worked out as 1 kg. Would that make a big difference?
Also what did you mean by subtracting the mass?