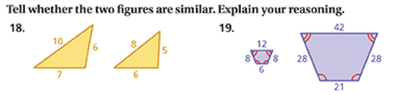MHB Determining similarity of plane figures
- Thread starter MathIsHard123
- Start date
-
- Tags
- Plane
Similar threads
- · Replies 8 ·
- · Replies 13 ·
- · Replies 3 ·
- · Replies 36 ·
- · Replies 6 ·
- · Replies 1 ·
- · Replies 10 ·
- · Replies 2 ·
- · Replies 5 ·
High School
4th spatial dimension thought experiment
- · Replies 8 ·