Determining stable and unstable equilibrium points

[chipotleaway]

Background:
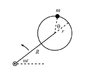
I've derived the equation of motion of the bead shown in the picture below using the Lagrangian
\omega^2Rsin(\theta)+r\ddot{\theta}=0
The equilibrium points are at θ=0 and π. I'm now to show that only one of these points is stable.

Homework Statement

Show that only one of the equilibrium points is stable against small deviations from equilibrium. Do so by considering small deviations \delta \theta=\theta-\theta_{equilibrium} from equilibrium.

The Attempt at a Solution

Rearranging the equation of motion for the acceleration \ddot{\theta}, we have \ddot{\theta}=-\frac{\omega^2R}{r}sin(\theta)

For small angles \theta deviating from 0, sin(θ)≈θ so the above equation becomes \ddot{theta}=-\frac{\omega^2R}{r}\theta. Similarly for deviations from angle of π, sin(θ-π)≈θ-π and therefore \ddot{\theta}=-\frac{\omega^2R}{r}\theta--\frac{\omega^2R}{r}\pi.

The latter is larger in magnitude than the former so the acceleration with be bigger and hence it's unstable (but this doesn't really prove anything, does it?). Don't know what I'm doing here!

 

[voko]

Please fix your equations.

The whole point of this "small deviations from equilibrium" business is to obtain the equation $\ddot x + a x = 0$, where $x$ is the small deviation. Then, depending on the sign of $a$, you either get oscillations (stable) or exponential blow-up (unstable).

 

[chipotleaway]

LaTeX isn't showing up for me for some reason - so I can't see what's wrong...

So the second derivative of a number? Does this method have a name?

 

[voko]

LaTeX isn't showing up for me for some reason - so I can't see what's wrong...

In many places, you did not put a backslash in front of theta and omega, so those are rendered as words, not as Greek letters. It is especially weird when you have \ddot on them.

So the second derivative of a number? Does this method have a name?

I do not understand what you said here.

 

[chipotleaway]

Ok, fixed for all the symbols I spotted.

Because in your post, you mentioned \ddot{x}+ax=0, where x is a small deviation - isn't a small deviation just some number? And you have the double dot to indicate time derivative.

 

[voko]

Well, you have equilibrium at $\theta = \theta_e$, then you can change variables via $\theta = x + \theta_e$ and obtain the equations for $x$ instead of $\theta$, taking into account that $x$ is small.

 

[chipotleaway]

Sorry, I'm not sure I follow. x is a variation from equilibrium angle \theta_e right? i.e. \delta \theta?

And what we want is an equation in terms of x? The substitution you mentioned just gives x=0 though doesn't it? And where did 'a' come from in your first post?

 

[voko]

Sorry, I'm not sure I follow. x is a variation from equilibrium angle \theta_e right? i.e. \delta \theta?

Correct.

And what we want is an equation in terms of x? The substitution you mentioned just gives x=0 though doesn't it?

How so? $\theta_e$ is a constant, not a variable.

And where did 'a' come from in your first post?

This is whatever you get after recasting the equation in terms of $x$ and using the "small deviation" approximation.

 

[chipotleaway]

I must've misinterpreted what you said - thought you meant make the substitution \theta=x+\theta_e and then sub it back into \theta=\theta_e[/tex].<br /> <br /> Could you please show or direct me to an example (or where I can read up on this)?

 

[voko]

Take your equation and let $\theta_e = \pi$. Then you have $\omega^2 R \sin (x + \pi) = r \ddot x$. All that you have to do is approximate the left hand side with something that is linear in $x$ (remember, x is assumed to be small).

 

[chipotleaway]

I couldn't figure it all out in time for my assignment but thanks for your help. Definitely something I will come back to after my exams

 

[voko]

Have a look here: http://en.wikipedia.org/wiki/List_of_trigonometric_identities#Shifts_and_periodicity , shift by $\pi$.